Filtro digitale
Nell’elaborazione delle immagini, un filtro elabora nel dominio della frequenza e si il tuo compito è passare, modificare o rigettare componenti di frequenza specifiche di un’immagine digitale. Può essere matematicamente concettualizzato come una funzione del tipo
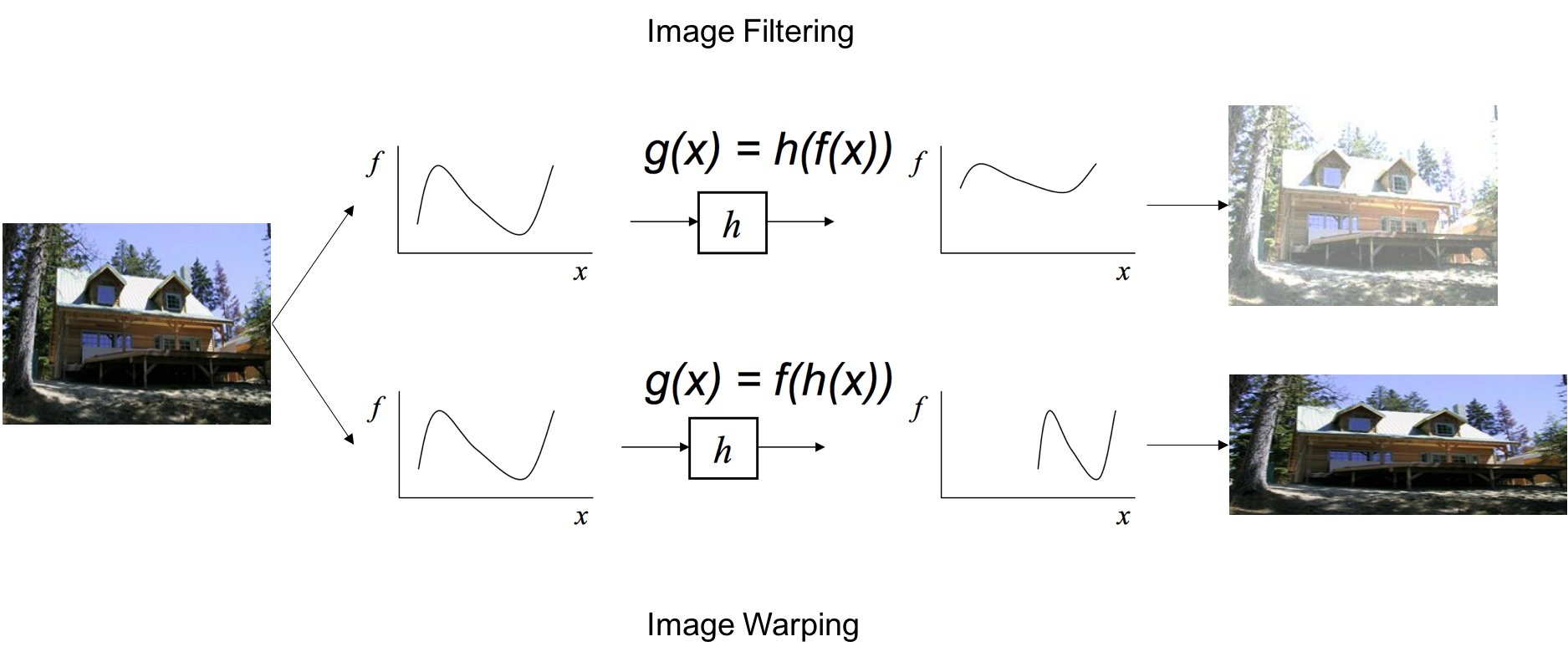
Tipi di filtro
I filtri si suddividono in base al dominio in cui operano:
Filtri spaziali
Il dominio spaziale (spatial filtering si riferisce al piano dell’immagine stessa, dove i metodi di elaborazione sono basati sulla manipolazione diretta dei pixel.
- Meccanica: il filtraggio spaziale modifica un’immagine sostituendo il valore di ciascun pixel con una funzione dei valori di quel pixel e dei suoi vicini. L’operazione viene eseguita su un’area ristretta (spesso rettangolare) chiamata vicinato o neighborhood.
- Nucleo del Filtro (Filter Kernel): In questo dominio, il filtro è rappresentato da una matrice chiamata nucleo del filtro (filter kernel), o anche maschera (mask), template o finestra.
- Filtri Lineari: Se l’operazione sui pixel è lineare, il filtro è detto filtro spaziale lineare. Un filtro spaziale lineare esegue un’operazione di somma dei prodotti (sum-of-products) tra l’immagine e il nucleo del filtro. Questa operazione è sinonimo di convoluzione spaziale (spatial convolution).
- Filtri Non Lineari: Altrimenti, il filtro è non lineare. Un esempio importante è il Filtro mediano (un filtro statistico d’ordine), la cui risposta si basa sull’ordinamento dei pixel nel vicinato; esso sostituisce il valore del pixel centrale con la mediana dei valori di intensità vicini. I filtri mediani sono particolarmente efficaci nel ridurre il rumore impulsivo (sale e pepe).
B. Filtri nel Dominio della Frequenza (Frequency Domain Filtering) Il filtraggio nel dominio della frequenza è una tecnica di elaborazione che richiede di eseguire una trasformata (come la Trasformata di Fourier Discreta, DFT) sull’immagine, eseguire l’elaborazione su tale dominio e, infine, calcolare la trasformata inversa per tornare al dominio spaziale.
- Funzione di Trasferimento del Filtro (
): Nel dominio della frequenza, il filtro è chiamato funzione di trasferimento del filtro. - Operazione Fondamentale: Il filtraggio in questo dominio si basa sulla moltiplicazione elemento per elemento della funzione di trasferimento del filtro
con la Trasformata di Fourier dell’immagine in ingresso, seguita dalla trasformata inversa per ottenere l’immagine filtrata . - Equivalenza Spazio-Frequenza: Il teorema di convoluzione stabilisce un’equivalenza tra il filtraggio nel dominio spaziale (convoluzione) e il filtraggio nel dominio della frequenza (moltiplicazione). Il nucleo spaziale
e la funzione di trasferimento nel dominio della frequenza formano una coppia di trasformate di Fourier. ]]