Automa finito deterministico (DFA)

Definizione di Automi finiti deterministici (DFA)

In informatica teorica un’automa a stati finito deterministico (DFA) è un modello di automa che soddisfano la condizione di determinismo, cioè per ogni coppia di stato e simbolo in ingresso, esiste una sola transizione possibile allo stato successivo.

Questo diagramma ha 3 stati (, e ). Gli archi che vanno da uno stato all’altro sono chiamati transizioni. L’output è accetta o rifiuta.

Definizione formale di DFA

Un DFA è definito formalmente come una quintupla: , dove:

1. è l’insieme finito degli stati dell’automa.
2. è l’alfabeto finito di simboli di input.
3. è la Funzione di transizione, che mappa coppie di uno stato e un simbolo di input a uno stato successivo. In altre parole, è completamente deterministica, fornendo una sola transizione possibile per ogni coppia stato-simbolo.
4. è lo stato iniziale dell’automa, .
5. è l’insieme degli stati accettanti o finali dell’automa, .

Ogni transizione è uno stato specifico verso cui l’automa transita quando si trova nello stato e legge un simbolo.

Come funziona?

1. L’automa riceve i simboli della stringa di input uno alla volta.
2. Per ogni simbolo letto, l’automa transita esattamente in uno stato successivo, determinato dalla funzione di transizione.
3. Se alla fine dell’input l’automa si trova in uno stato accettante, la stringa è accettata; altrimenti, è rifiutata.

Un DFA è completamente deterministico, il che significa che, dato uno stato e un simbolo di input, esiste un’unica transizione possibile.

Determinismo

Quando la macchina è in un dato stato e legge il simbolo di input successivo, lo stato successivo sarà univocamente determinato. Ogni automa finito deterministico è automaticamente un automa finito non deterministico in quanto il determinismo è una generalizzazione del non determinismo.

Cosa sono le operazioni regolari?

Sinoa e dei linguaggi. Definiamo le operazioni regolari unione, concatenazione, e star come segue:

• L’operazione unione () prende tutte le stringhe sia in che in e le raggruppa insieme in un linguaggio.
• L’operazione concatenazione antepone una stringa di A ad una stringa d B in tutti i modi possibili per ottenere le stringhe nel nuovo linguaggio.
• L’operazione star (*) è un’operazione unaria invece che binaria: opera concatenando un numero qualsiasi (compreso 0) di stringhe in A insieme per ottenere una stringa nel nuovo linguaggio.

Catene di Markov

Gli automi finiti e la loro controparte probabilistica, le catene di Markov, sono utili per riconoscere pattern in dati. Utilizzati ad esempio nell’elaborazione vocale e nel riconoscimento ottico.

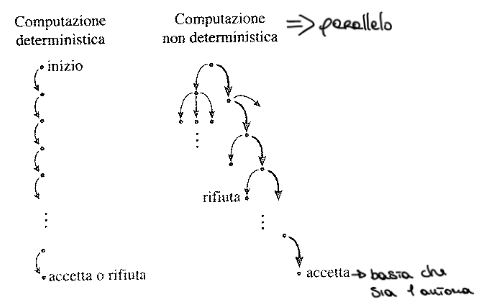
Automi finiti non deterministici (NFA)

🔛 Comparazione tra DFA e NFA

❌ Differenze tra DFA e NFA

1. Funzione di Transizione:
   • DFA: La funzione di transizione δ in un DFA restituisce uno stato singolo per ogni coppia stato e simbolo di input.
   • NFA: La funzione di transizione δ in un NFA restituisce un insieme di possibili stati successivi per ogni coppia stato e simbolo di input, incluso il simbolo di input vuoto (ε).
2. Determinismo:
   • DFA: È completamente deterministico, ovvero, per una specifica combinazione di stato e simbolo di input, esiste una sola transizione possibile.
   • NFA: È non deterministico, il che significa che per una specifica combinazione di stato e simbolo di input, ci possono essere più transizioni possibili.
3. Numero di Transizioni:
   • DFA: Ha esattamente una transizione per ogni coppia di stato e simbolo di input.
   • NFA: Può avere zero, una, o più transizioni per ogni coppia di stato e simbolo di input.
4. Stati Accettanti:
   • DFA: Gli stati accettanti sono chiaramente definiti, e un input viene accettato se lo stato finale è uno degli stati accettanti.
   • NFA: Un input viene accettato se almeno una delle possibili computazioni termina in uno stato accettante.
     

Attenzione!

Un NFA può essere molto più piccolo della sua controparte deterministica.

✔️ Somiglianze tra DFA e NFA

1. Linguaggi Riconosciuti:
   • DFA e NFA: Entrambi riconoscono lo stesso insieme di linguaggi regolari. Ogni linguaggio riconosciuto da un NFA può essere riconosciuto da un DFA equivalente e viceversa.
     
2. Equivalenza tra DFA e NFA:
   • Ogni NFA ha un DFA equivalente: Per ogni automa finito non deterministico (NFA), esiste un automa finito deterministico (DFA) equivalente che riconosce lo stesso linguaggio.
     
3. Conversione da NFA a DFA:
   • DFA può simulare un NFA: Gli NFA possono essere convertiti in DFA, mantenendo l’equivalenza nei linguaggi riconosciuti. Questo processo è noto come la “conversione subset” o “costruzione dei sottoinsiemi”.

🔃 Conversione da automa finito a Regex

Teorema di Equivalenza di Kleene: questo teorema stabilisce che, per ogni espressione regolare, esiste un automa a stati finiti che riconosce il linguaggio regolare descritto dall’espressione, e viceversa.

Da Espressione Regolare a Automa Finito

1. Definizione dell’Alfabeto e della Struttura: identificare l’alfabeto sui cui opererà l’automa e strutturare gli stati dell’automa per rappresentare il processo di riconoscimento.
   
2. Traduzione delle Espressioni Regolari in Automi Finiti: ogni parte dell’espressione regolare viene tradotta in una struttura dell’automa corrispondente.
   
3. Combinazione delle Strutture: combinare le strutture degli automi corrispondenti alle diverse parti dell’espressione regolare per ottenere un’automa completo che riconosca il linguaggio descritto dall’espressione.
   

Da Automa Finito a Espressione Regolare

1. Definizione dell’Alfabeto e degli Stati: identificare l’alfabeto dell’automa e gli stati coinvolti nel riconoscimento del linguaggio.
   
2. Applicazione del Teorema di Equivalenza di Kleene: utile per derivare un’espressione regolare che descriva il linguaggio riconosciuto dall’automa. Questo coinvolge la costruzione di un sistema di equazioni basato sugli stati e le transizioni dell’automa.
   
3. Risoluzione delle Equazioni: risolvere il sistema di equazioni per ottenere un’espressione regolare equivalente.
   

Cos'è un linguaggio regolare?

Un linguaggio regolare è un insieme di stringhe di simboli, costruite su un alfabeto finito, che può essere descritto o riconosciuto mediante un’espressione regolare o attraverso l’azione di un automa a stati finiti, come un DFA o un NFA.

Esempio con NFA

Consideriamo l’espressione regolare seguente:

Questa espressione regolare descrive il linguaggio di tutte le stringhe che contengono zero o più occorrenze di o seguite da un . Adesso creeremo un NFA equivalente.

1. Definizione dell’Alfabeto:
2. Creazione degli Stati:
   • Stato Iniziale:
   • Stato Finale:
3. Aggiunta delle Transizioni:
   • Dallo stato iniziale ​, aggiungiamo una transizione etichettata con (la transizione vuota) verso uno stato intermedio .
   • Da , aggiungiamo transizioni etichettate con e verso ​ stesso (rappresentando il loop per zero o più occorrenze di o .
   • Aggiungiamo una transizione etichettata con da ​ allo stato finale ​.
   • Infine, da ​ aggiungiamo una transizione etichettata con verso uno stato finale aggiuntivo (per indicare che è l’ultimo carattere richiesto).

Esempio con DFA

Pumping Lemma

Si può provare la regolarità o meno di un linguaggio con un teorema chiamato pumping lemma.

Questo teorema afferma che tutti i linguaggi regolari hanno una proprietà speciale. Se possiamo dimostrare che un linguaggio non ha questa proprietà, siamo sicuri che esso non è regolare.

La proprietà afferma che tutte le stringhe nel linguaggio possono essere “replicate” se la loro lunghezza raggiunge almeno uno specifico valore speciale, chiamato lunghezza di pumping.

Lunghezza di pumping

La “lunghezza di pumping” è un valore critico che rappresenta la lunghezza minima a cui una stringa può essere suddivisa e ripetuta per ottenere ancora una stringa appartenente al linguaggio. Questo valore è specifico per ciascun linguaggio e viene determinato dal “Pumping Lemma”.

Il “Pumping Lemma” afferma che qualsiasi stringa (dove è un numero naturale) deve ancora appartenere al linguaggio. Ciò significa che la parte può essere ripetuta o eliminata mantenendo la stringa nel linguaggio. ha almeno lunghezza equivalente alla lunghezza di pumping.