Classi di complessità (P, NP, NP-completi)

Definizione di classi di complessità (P, NP, NP-Completi)

I problemi computazionali sono raggruppati in classi in base all’efficienza degli algoritmi che li risolvono o li verificano.

1. Classe P (Polinomiale):

   • Contiene i problemi di decisione che possono essere risolti da un algoritmo in tempo polinomiale. Questo significa che esiste un algoritmo tale che il suo tempo di esecuzione è per qualche costante , dove è la dimensione dell’input.
   • Intuitivamente, i problemi in P sono considerati “facili” o “trattabili” per un calcolatore.
   • Esempio Pratico: L’ordinamento di un array con algoritmi come MergeSort () o CountingSort () rientra in P. Anche la ricerca di cammini minimi su grafi senza pesi negativi con Dijkstra () o su DAG () sono problemi in P.

2. Classe NP (Nondeterministic Polynomial time):

   • Contiene i problemi di decisione per i quali, data una possibile soluzione, è possibile verificare la sua correttezza in tempo polinomiale.
   • Un algoritmo di verifica accetta due argomenti: una stringa di input e una stringa binaria chiamata certificato. se il certificato dimostra che appartiene al linguaggio associato al problema.
   • Esempio Pratico: Consideriamo il problema del Ciclo Hamiltoniano (HAM-CYCLE), che chiede se esiste un ciclo semplice che tocca ogni vertice di un grafo. Trovare tale ciclo è difficile (“attualmente” non esiste un algoritmo polinomiale), ma se ti viene fornita una sequenza di vertici (il certificato ), puoi verificare in tempo polinomiale se è un ciclo hamiltoniano: basta controllare che tutti i vertici del grafo siano inclusi e che esista un arco per ogni coppia di vertici adiacenti nella sequenza. Quindi, HAM-CYCLE è in NP.
   • La classe P è un sottoinsieme proprio di NP, poiché un problema risolvibile in tempo polinomiale è anche verificabile in tempo polinomiale.

La Questione P vs NP

La domanda se (ovvero, se tutti i problemi la cui soluzione può essere verificata rapidamente possano anche essere risolti rapidamente) è uno dei problemi aperti più importanti dell’informatica teorica. Attualmente si ritiene che , il che implicherebbe che i problemi in NP ma non in P sono “intrattabili” o “difficili” nel senso che non esistono algoritmi polinomiali per risolverli.

Classe NP-Completi (NP-C) e Riducibilità Polinomiale

I problemi NP-Completi sono il “cuore” della classe NP. Essi sono definiti da due proprietà fondamentali:

1. Il problema appartiene alla classe NP.
2. È possibile ridurre qualsiasi altro problema in NP a questo problema in tempo polinomiale. Questo significa che se si trovasse un algoritmo polinomiale per risolvere un singolo problema NP-Completo, allora ogni problema in NP sarebbe risolvibile in tempo polinomiale, implicando .

Il concetto di riducibilità polinomiale () è cruciale: significa che esiste una funzione calcolabile in tempo polinomiale tale che se e solo se . In altre parole, un’istanza del problema può essere trasformata in tempo polinomiale in un’istanza del problema , in modo tale che la soluzione di risolva anche . Il Lemma 2 afferma che se e , allora .

I problemi NP-Difficili sono quei problemi che soddisfano solo la seconda condizione della NP-completezza, ovvero qualsiasi problema in NP è riducibile a essi in tempo polinomiale, ma non è detto che essi stessi siano in NP. Possono essere anche più complessi della verifica polinomiale.

La dimostrazione che un problema è NP-Completo spesso segue questi passi:

1. Dimostrare che il problema è in NP (ovvero, la sua soluzione è verificabile in tempo polinomiale).
2. Dimostrare che il problema è NP-Difficile, scegliendo un problema già noto essere NP-Completo e descrivendo un algoritmo che riduce al problema in questione in tempo polinomiale.

Esempi di Problemi NP-Completi

La teoria della NP-completezza è stata fondata con la dimostrazione che Circuit-SAT (soddisfacibilità di un circuito logico) è NP-Completo. Da qui, una “catena” di riduzioni ha permesso di classificare molti altri problemi come NP-Completi.

1. Circuit-SAT: Problema di decisione che valuta se, dati certi input booleani, un circuito logico produce un output 1 (soddisfacibile). È in NP (verificabile in tempo polinomiale) ed è NP-Difficile (qualsiasi problema in NP è riducibile a esso).
2. SAT (Satisfiability): Verifica la soddisfacibilità di una formula booleana generale. Una formula è soddisfacibile se esiste almeno un’assegnazione di verità alle sue variabili che la rende vera. SAT è NP-Completo perché è in NP (verificabile sostituendo valori) e Circuit-SAT è riducibile a SAT.
3. 3-CNF-SAT (o 3-SAT): Simile a SAT, ma la formula booleana deve essere in forma normale congiuntiva (CNF) e ogni clausola (disgiunzione di letterali) deve contenere esattamente 3 letterali. È NP-Completo perché è in NP e SAT è riducibile a 3-SAT.
4. CLIQUE: Dato un grafo non orientato e un intero , decide se contiene una cricca (sottografo completo) di dimensione . È NP-Completo perché è in NP e 3-SAT è riducibile a CLIQUE.
5. VERTEX-COVER: Dato un grafo non orientato e un intero , decide se ha una copertura di vertici di dimensione . Una copertura di vertici è un sottoinsieme di vertici tale che ogni arco in ha almeno un estremo in . È NP-Completo perché è in NP e CLIQUE è riducibile a VERTEX-COVER.
6. HAM-CYCLE (Ciclo Hamiltoniano): Dato un grafo , decide se esiste un ciclo semplice che contiene ogni vertice di . È NP-Completo perché è in NP e VERTEX-COVER è riducibile a HAM-CYCLE.
7. TSP (Traveling Salesperson Problem): Estensione di HAM-CYCLE su grafi pesati. Dato un grafo pesato e un costo massimo , decide se esiste un ciclo hamiltoniano con costo totale minore o uguale a . È NP-Completo perché è in NP e HAM-CYCLE è riducibile a TSP.

In sintesi, la classificazione dei problemi in P, NP, NP-Completi e NP-Difficili è fondamentale per comprendere i limiti intrinseci della computazione, guidando la ricerca di algoritmi efficienti per i problemi “facili” e spingendo verso l’uso di euristiche o algoritmi approssimati per quelli “difficili”.

Cosa sono le classi di complessità

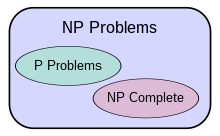
Problemi NP

Problemi P

Questo tipo di problema è una sottoclasse dei problemi NP. Problemi per cui esiste un algoritmo in grado di risolverli in tempo polinomiale. Verificabile in tempo polinomiale.

Problemi NP-completi

SAT (soddisfacibilità booleana)

https://it.wikipedia.org/wiki/Soddisfacibilit%C3%A0_booleana

Il SAT è stato il primo NP-completo.

Il problema SAT consiste nel verificare la soddisfacibilità delle formule booleane. In base a quanti sono i connettivi logici facciamo operazioni Un’istanza SAT è formata da una formula booleana :

• n variabili booleane
• m connettivi booleani
• Parentesi

La soddisfacibilità di una formula booleana è un problema NP-difficile.

3-SAT

Il 3-SAT è un problema NP-completo. Definiamo Andremo a costruire un albero binario:

• nelle foglie poniamo i letterali Se abbiamo due letterali (P, Q) consideriamo solo P

Circuit-SAT

Problema NP-completo. Un circuito logico è formato da:

• Porte logiche: prendono degli input booleani, lavorano funzioni booleane
• Cavi: trasportano gli output da una porta all’altra

Cricca

Dato un grafo G=(V,E)

Vertex Cover

• Cos’è la cardinalità?
• Cos’è un grafo complementare? (https://it.wikipedia.org/wiki/Grafo_complemento)