Hash table

Una Hash table (o tabella hash) è una struttura dati usata per mettere in corrispondenza una data chiave con un dato valore. Viene usata per l’implementazione di strutture astratte associative come le mappe o i set.

• Hashing universale: Una famiglia di funzioni hash da cui scegliere una funzione casuale per rendere gli attacchi avversari inefficaci.

• Tabelle ad indirizzamento diretto: Una variante più semplice dove le chiavi sono usate direttamente come indici. Efficienza O(1) per INDEX, ma soffre di spreco di spazio se l’universo delle chiavi U è molto più grande delle chiavi effettivamente usate.

• Descrizione: Superano i limiti delle tabelle a indirizzamento diretto mappando un sottoinsieme di chiavi K su un intervallo di indici [0, …, m-1] tramite una funzione hash h(k). Questo può generare collisioni (chiavi diverse mappano allo stesso indice).

  • Metodi di Risoluzione delle Collisioni:
    • Concatenamento (Chaining): Utilizza liste concatenate. Se più chiavi mappano alla stessa cella h(k), gli elementi sono memorizzati in una lista concatenata a partire da quella cella.
      • Complessità (caso medio, assumendo hashing uniforme e indipendente):
        • SEARCH, INSERT, DELETE: O(1 + α), dove α = n/m è il fattore di carico (numero medio di elementi per lista).
        • INSERT e SEARCH sono tipicamente O(1) se n è proporzionale a m (quindi α è O(1)).
      • Complessità (caso peggiore): Se tutte le chiavi collidono, degenera a una lista concatenata, quindi O(n).
    • Indirizzamento Aperto (Open Addressing): Le collisioni vengono gestite cercando la prima posizione libera nella tabella. Se una cella è occupata, si ispezionano altre celle secondo una sequenza predefinita.
      • DELETE è molto delicata, richiede l’uso di valori speciali (DELETE) per non compromettere le ricerche future.
      • Funzioni Hash (per indirizzamento aperto):
        • Linear Probing (Scansione Lineare): h(k, i) = (h'(k) + i) mod m. Esplora le celle linearmente dopo la prima collisione. Efficiente in pratica per via della cache.
        • Double Hashing (Doppio Hashing): h(k, i) = (h1(k) + i * h2(k)) mod m. Utilizza due funzioni hash ausiliarie per generare una sequenza di ispezione più complessa. Richiede che h2(k) sia coprimo con m.
      • Complessità (caso medio, con permutazioni uniformi e indipendenti, senza cancellazioni):
        • SEARCH (senza successo) e INSERT: al più O(1 / (1 - α)).
        • SEARCH (con successo): al più O(1/α * ln(1/(1-α))).

Hashing

Utilizzata nei metodi di ricerca chiamati hashing ovvero un’estensione della ricerca indicizzata da chiavi che gestisce problemi di ricerca nei quali le chiavi di ricerca non presentano queste proprietà.

Costo di ricerca

in una tabella di hashing ben dimensionata il costo medio di ricerca di ogni elemento è indipendente dal numero di elementi

Una ricerca basata su hashing è diversa da una basata su confronti: invece di muoversi nella struttura data in funzione dell’esito dei confronti tra chiavi, si cerca di accedere agli elementi nella tabella in modo diretto tramite operazioni aritmetiche che trasformano le chiavi in indirizzi della tabella.

Collisione: Il caso in cui la funzione hash applicata a due chiavi diverse genera un medesimo indirizzo.

• Progettazione di Funzioni Hash Efficienti:
  • Hashing Statico: Funzione hash unica, basata sulla distribuzione dei dati. Metodi comuni: divisione (k mod m) e moltiplicazione (m * (k * A mod 1)). Vulnerabile ad attacchi.
  • Hashing Randomizzato (Universale): Utilizza una famiglia di funzioni hash H e ne seleziona una casualmente all’inizio, rendendo impossibile per un attaccante forzare il caso peggiore. Una famiglia H_ab(k) = (a*k + b mod p) mod m è universale.
• Utilizzo Pratico: Implementazione di dizionari, insiemi, caching. Usate anche nella ricerca Best-First.

Open Hash

Nell’ indirizzamento aperto tutti gli elementi sono memorizzati nella tavola hash stessa; ovvero ogni cella della tavola contiene un elemento dell’insieme dinamico o la costante NULL.

Vantaggi

Il vantaggio dell’indirizzamento aperto sta nel fatto che esclude completamente i puntatori, calcoliamo la sequenza delle celle da esaminare (ispezione)

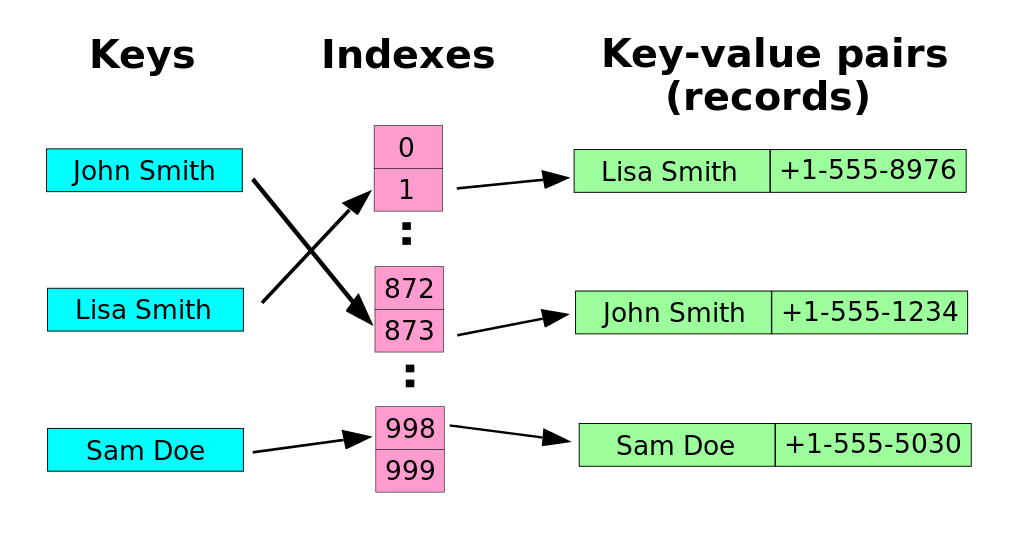
Le tabelle hash rappresentano una soluzione efficiente per l’organizzazione di insiemi dinamici, superando i limiti delle Tabelle a indirizzamento diretto in termini di spazio e flessibilità. Le tabelle hash mappano un sottoinsieme K dell’universo U di chiavi in un intervallo [0, …, m-1] di indici tramite una funzione hash h: U -> {0, 1, …, m-1}.

Collisioni e risoluzione

Il problema principale delle tabelle hash è la collisione, che si verifica quando due chiavi distinte k1 e k2 sono mappate allo stesso indice, ovvero h(k1) = h(k2). Una funzione hash ideale dovrebbe generare immagini in modo “casuale” e indipendente per minimizzare la probabilità di collisioni, sebbene non possa annullarle.

Per risolvere le collisioni, si possono adottare diverse strategie:

1. Concatenamento (Chaining): Questo metodo prevede l’utilizzo di una struttura dati ausiliaria, tipicamente una lista concatenata, per ogni cella della tabella hash. Se più elementi collidono sullo stesso indice h(k), essi vengono inseriti nella lista associata a quella cella. La cella quindi punta alla testa della lista. Le operazioni di inserimento avvengono solitamente in testa alla lista per semplicità. Con un’adeguata distribuzione degli elementi, l’operazione di INDEX (ricerca) può raggiungere una complessità media di O(1).

   • Analisi Caso Medio per Concatenamento: Si definisce il fattore di carico α = n/m, dove n è il numero di elementi e m il numero di celle, indicando il numero medio di elementi per lista.
     • Per una ricerca senza successo, in media, il tempo è Θ(1 + α). Questo perché, ipotizzando una funzione hash uniforme e indipendente, la ricerca richiede il tempo per calcolare h(k) (Θ(1)) più il tempo per percorrere la lista associata (Θ(α)).
     • Anche per una ricerca con successo, in media, il tempo è Θ(1 + α). Questo deriva dal fatto che, cercando un elemento x, si devono esaminare 1 + il numero di elementi inseriti dopo x che collidono con x nella stessa cella.

2. Indirizzamento Aperto (Open Addressing): A differenza del concatenamento, l’indirizzamento aperto non utilizza strutture dati esterne per le collisioni. Se una cella q = h(k) è già occupata, si cerca la prima posizione libera nella tabella seguendo una sequenza di ispezione predefinita. La funzione hash viene generalizzata come h(k, i), dove i è il numero di tentativi di ispezione (0, …, m-1), e la sequenza h(k, 0), h(k, 1), …, h(k, m-1) deve essere una permutazione delle m celle.

   • Tecniche di Ispezione:
     • Ispezione Lineare (Linear Probing): La sequenza di ispezione è h(k, i) = (h'(k) + i) mod m. Qui, h'(k) è una funzione hash ausiliaria e i è l’offset incrementale. Questo metodo genera solo m permutazioni possibili (la sequenza di ispezione è una progressione lineare). Sebbene teoricamente meno efficiente nel caso peggiore (O(n) per una ricerca), in pratica è spesso efficiente grazie al modello di memoria gerarchica dei moderni calcolatori.
     • Doppio Hashing (Double Hashing): Utilizza due funzioni hash ausiliarie, h1(k) e h2(k), per generare la sequenza di ispezione: h(k, i) = (h1(k) + i * h2(k)) mod m. Per garantire che tutte le m celle siano esaminate, h2(k) deve essere coprimo con m. Questo metodo genera m^2 permutazioni possibili, riducendo l’insorgere di raggruppamenti primari.
   • Cancellazione (Delete): L’operazione di DELETE è particolarmente delicata nell’indirizzamento aperto. Semplicemente mettendo a NIL un elemento cancellato si potrebbe interrompere la sequenza di ispezione per elementi precedentemente inseriti, rendendoli irraggiungibili. Si ricorre quindi all’uso di un valore DELETE speciale che viene trattato come NIL durante l’inserimento, ma come una cella occupata durante la ricerca.
   • Analisi della Ricerca senza Successo per Indirizzamento Aperto: Sotto l’ipotesi di permutazioni generate uniformemente e indipendentemente e in assenza di cancellazioni, il numero atteso di operazioni per una ricerca senza successo (E[X]) in una tabella con fattore di carico α = n/m < 1 è al più 1 / (1 - α).
     • Sia X la variabile casuale che indica il numero di ispezioni. Sia Ai l’evento che all’ispezione i si incontra una cella piena.
     • La probabilità che la prima ispezione (A1) trovi una cella piena è n/m (poiché n elementi sono distribuiti in m celle).
     • La probabilità che la j-esima ispezione (Aj) trovi una cella piena, dato che le j-1 ispezioni precedenti hanno trovato celle piene, è (n - (j-1)) / (m - (j-1)). Questo perché restano n - (j-1) elementi da cercare in m - (j-1) celle non ancora esaminate.
     • Quindi, Pr(X >= i) è la probabilità che le prime i-1 celle ispezionate siano piene, data da (n/m) * ((n-1)/(m-1)) * … * ((n-i+2)/(m-i+2)).
     • Questa probabilità è Pr(X >= i) <= (n/m)^(i-1) = α^(i-1).
     • Il valore atteso E[X] è dato dalla somma delle probabilità Pr(X >= i) per i da 1 a m (poiché al massimo m ispezioni sono possibili). E[X] = Σ(i=1 to m) Pr(X >= i).
     • Considerando la serie geometrica Σ(i=0 to m-1) α^i, la somma è (1 - α^m) / (1 - α). Poiché α < 1, per m tendente all’infinito o in approssimazione, E[X] <= 1 / (1 - α).
     • Questo significa che il tempo di ricerca per una chiave non presente è proporzionale a 1/(1-α). Ad esempio, se α = 0.5, il tempo è 2 operazioni, mentre se α = 0.9, sale a 10 operazioni.

Randomizzazione e Famiglie Universali

Per superare la vulnerabilità dell’hashing statico (dove un avversario che conosce la funzione può forzare collisioni, portando la ricerca a O(n)), si utilizza l’hashing randomizzato o hashing universale. L’idea è selezionare una funzione hash casualmente da una famiglia di funzioni hash H all’inizio di ogni esecuzione, rendendo impossibile per un avversario prevedere quale funzione verrà usata e quindi impedendogli di creare input che generino sistematicamente il caso peggiore.

Le famiglie di funzioni hash possono avere diverse proprietà:

• Uniforme: Una famiglia H è uniforme se per ogni chiave k in U e per ogni cella q in [0, …, m-1], la probabilità che h(k) = q sia 1/m.
• Universale: Una famiglia H è universale se per ogni coppia di chiavi distinte k1 e k2 in U, la probabilità di collisione h(k1) = h(k2) è al più 1/m.
• ε-universale: Generalizzazione dell’universalità, dove la probabilità di collisione è al più ε.
• d-indipendente: Una famiglia H è d-indipendente se per ogni scelta di d chiavi diverse k1, …, kd in U e d celle q1, …, qd (non necessariamente diverse), la probabilità che h(ki) = qi per tutti gli i è al più 1/m^d.

Progettazione di una Famiglia Universale: h_ab(k) = ((ak + b) mod p) mod m

Si può costruire una famiglia universale H_p,m scegliendo un numero primo p sufficientemente grande tale che ogni chiave k sia compresa nell’intervallo [0, p-1], e p > m (dove m è il numero di celle della tabella). La funzione hash è definita come h_a,b(k) = ((ak + b) mod p) mod m, dove a è scelto da [1, p-1] e b da [0, p-1]. La famiglia H_p,m contiene p(p-1) funzioni hash.

Dimostrazione dell’Universalità:

Consideriamo due chiavi distinte k1 e k2 nell’intervallo [0, p-1]. Per una data funzione h_a,b, definiamo: r1 = (ak1 + b) mod p r2 = (ak2 + b) mod p

Poiché p è un numero primo, se k1 != k2, allora (k1 - k2) mod p != 0. Di conseguenza, a(k1 - k2) mod p != 0 (dato che a != 0). Questo implica che r1 - r2 = a(k1 - k2) mod p != 0, e quindi r1 != r2. Ciò significa che ogni coppia (a, b) genera una coppia unica (r1, r2) di valori distinti modulo p.

Inoltre, è possibile ricavare a e b da r1 e r2: a = (r1 - r2) (k1 - k2)^(-1) mod p b = (r1 - a*k1) mod p Questa biunivocità implica che ogni coppia (r1, r2) di valori distinti modulo p corrisponde a una e una sola coppia (a, b). Poiché ci sono p possibili valori per r1 e p-1 valori per r2 (dato r1 != r2), ci sono p(p-1) coppie (r1, r2) distinte. Questa corrispondenza biunivoca garantisce che, scegliendo a e b casualmente e uniformemente, anche la coppia (r1, r2) è scelta casualmente e uniformemente tra tutte le p(p-1) possibili coppie distinte.

Una collisione h_a,b(k1) = h_a,b(k2) si verifica quando r1 mod m = r2 mod m. Senza perdere generalità, possiamo fissare r1. Ci sono p-1 possibili valori per r2 (tutti i valori in [0, p-1] tranne r1). Di questi p-1 valori, quanti collidono con r1 modulo m? Il numero di valori r' in [0, p-1] tali che r' mod m = r1 mod m è dato da ⌊(p-1-r1 mod m)/m⌋ + 1. Questo è approssimativamente p/m. Il numero di valori r2 != r1 tali che r2 mod m = r1 mod m è al più p/m - 1 (se r1 mod m è uno dei valori, altrimenti p/m). La probabilità di collisione è data da: (Numero di r2 che collidono con r1) / (Numero totale di r2 possibili). Considerando che ci sono p(p-1) coppie (r1,r2) e che per ogni coppia (r1, r2) la probabilità che r1 mod m = r2 mod m è al più (p + m - 1)/m - 1 = p/m - 1. La dimostrazione precisa indica che la probabilità di collisione per h_a,b(k1) = h_a,b(k2) è al più (p - 1) / (m * (p - 1)) = 1/m. Questo conferma che la famiglia H_p,m è universale.