Definizione di distribuzione normale
La distribuzione normale è una distribuzione di probabilità continua che descrive come sono distribuiti i valori di una variabile casuale reale. È rappresentata da una curva a forma di campana, simmetrica rispetto alla media.
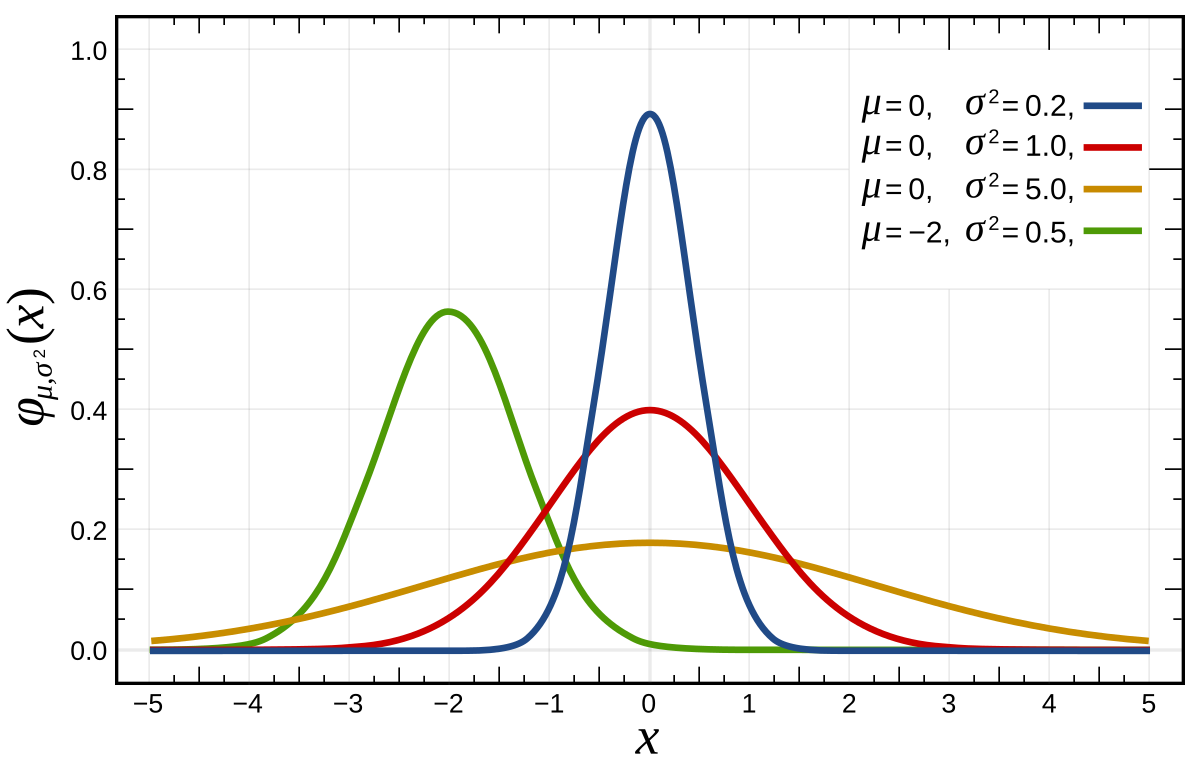
Caratteristiche principali
-
Forma a campana (curva gaussiana): la maggior parte dei dati si concentra attorno alla media.
-
Simmetria: la curva è perfettamente simmetrica rispetto alla media (μ).
-
Media = Mediana = Moda
-
Due parametri principali:
-
μ (mu): la media, che determina la posizione della curva.
-
σ (sigma): la deviazione standard, che determina l’ampiezza (larghezza) della curva.
-
🔢 Formula della densità della normale
La funzione di densità di probabilità (pdf) della normale è:
f(x)=1σ2πe−12(x−μσ)2f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{ -\frac{1}{2} \left( \frac{x - \mu}{\sigma} \right)^2 }
Dove:
-
xx è la variabile casuale
-
μ\mu è la media
-
σ\sigma è la deviazione standard
-
ee è il numero di Nepero (≈ 2.718)
📊 Esempio visivo (immaginario)
Supponiamo che l’altezza delle persone in una popolazione segua una distribuzione normale:
-
Media μ=170\mu = 170 cm
-
Deviazione standard σ=10\sigma = 10 cm
La maggior parte delle persone avrà un’altezza compresa tra 160 cm e 180 cm, cioè entro ±1 σ dalla media.
📈 Regola empirica (68-95-99.7)
In una distribuzione normale:
-
Circa 68% dei valori è compreso tra μ±1σ\mu \pm 1\sigma
-
Circa 95% tra μ±2σ\mu \pm 2\sigma
-
Circa 99.7% tra μ±3σ\mu \pm 3\sigma
📌 A cosa serve?
La distribuzione normale è usata in tantissimi contesti, ad esempio:
-
Nella teoria dell’inferenza statistica (test, intervalli di confidenza)
-
Per modellare fenomeni naturali (altezza, pressione, errori di misura)
-
Come approssimazione in molti teoremi (es. Teorema Centrale del Limite)