Data science

http://www.r-project.it/_book/clustering-gerarchico-agglomerativo-hc.html

La scienza dei dati segue un processo strutturato, a passi distinti, che, se adottato correttamente, preserva l’integrità dei risultati. I cinque passi fondamentali per la scienza dei dati sono:

1. Porre una domanda interessante: Iniziate a scrivere le domande indipendentemente dal fatto che pensiate che esistano i dati per rispondere a tali domande.
2. Ottenere i dati: Dopo aver scelto la domanda sulla quale concentrarvi, è il momento di considerare dove trovare i dati che consentirebbero di rispondere a tale domanda.
3. Esplorare i dati: Una volta in possesso dei dati, iniziate a catalogare i tipi di dati che avete a disposizione.
4. Creare un modello per i dati: Questo passo coinvolge l’uso di modelli statistici e di machine learning.
5. Comunicare e presentare i risultati: Anche se potrebbe sembrare ovvio e semplice, la capacità di concludere la ricerca e presentare i vostri risultati in una forma chiara e comprensibile è molto più difficile di quanto si possa immaginare.

Cosa sono i dati?

I dati sono una raccolta di informazioni, organizzate o meno. La scienza dei dati si occupa di estrarre conoscenza dai dati e utilizzarla per prendere decisioni, fare previsioni e comprendere il presente e il passato. I dati possono presentarsi in diverse forme, con diversi livelli di organizzazione e tipi. Possono essere:

• Strutturati: organizzati in tabelle con righe e colonne, come ad esempio i dati presenti in un foglio di calcolo.
• Non strutturati: privi di un’organizzazione standard, come ad esempio il testo libero.
• Quantitativi: espressi tramite numeri e utilizzabili per operazioni matematiche.
• Qualitativi: descritti da categorie o nomi e non analizzabili matematicamente.

I dati, inoltre, possono essere classificati in quattro livelli in base alla loro complessità e alle operazioni matematiche applicabili: nominale, ordinale, a intervalli e a rapporti. Capire il tipo e il livello dei dati è fondamentale per scegliere i metodi di analisi e ottenere risultati significativi.

L’importanza della qualità dei dati

La qualità dei dati è fondamentale nella scienza dei dati, l'utilizzo di dati mancanti o errati potrebbe impedire la riuscita di una buona analisi dati.

• Importanza della struttura dei dati: E’ importante determinare se i dati sono organizzati o non organizzati come primo passo nell’esplorazione dei dati.
  • I dati organizzati, strutturati in righe e colonne, sono generalmente più facili da analizzare rispetto a quelli non organizzati.
  • La pre-elaborazione dei dati, come la trasformazione di testo non strutturato in un formato strutturato, è spesso necessaria.
• Gestione dei dati mancanti: In casi d’uso reali i dati sono spesso imperfetti e possono presentare valori mancanti. Si deve quindi decidere come gestire queste lacune, ad esempio eliminando le righe con valori mancanti o cercando di completarle, considerando attentamente l’impatto di tali scelte sull’analisi.
• Trasformazione dei dati: Le trasformazioni dei dati sono spesso necessarie in base al tipo e al livello dei dati.
  • Ad esempio, la conversione di caratteristiche categoriche in quantitative tramite l’uso di variabili fittizie è una tecnica comune per preparare i dati per la modellazione.
• Importanza della pulizia dei dati nel machine learning: I modelli di machine learning richiedono generalmente dati “puliti” (privi di valori mancanti o categorici).
  • La mancata pre-elaborazione e pulizia dei dati può portare a modelli inaccurati o fuorvianti.

L’analisi esplorativa dei dati (EDA)

L’analisi esplorativa dei dati (EDA) è un passo fondamentale nel processo di scienza dei dati che mira a preparare i dati per la successiva fase di modellazione. Può essere intesa come l’arte di riconoscere i diversi tipi di dati, trasformare i tipi di dati e usare il codice per migliorare la qualità dell’intero set di dati.

Domande chiave nell’analisi esplorativa

Quando si affronta un nuovo set di dati è utile porsi una serie di domande:

1. I dati sono organizzati o no?
   • Questo implica determinare se i dati sono strutturati in righe e colonne (dati organizzati) o se si presentano in un formato meno strutturato. I dati non organizzati spesso richiedono una fase di pre-elaborazione per essere trasformati in un formato strutturato, come righe e colonne.
2. Cosa rappresenta ogni riga?
   • Una volta compreso il formato dei dati, è importante identificare cosa rappresenta ogni riga del set di dati. Questa fase aiuta a contestualizzare i dati e a comprenderne il significato.
3. Cosa rappresenta ogni colonna? Per ogni colonna, è necessario identificare:
   • il tipo di dati (quantitativo o qualitativo)
   • il livello dei dati (nominale, ordinale, a intervalli, a rapporti)
   • la presenza di dati mancanti
   • la necessità di trasformazioni.

Trasformazioni e analisi preliminare

L'analisi esplorativa dei dati è un processo iterativo e investigativo che mira a comprendere la struttura e il contenuto dei dati e identificare eventuali problemi di qualità dei dati. Durante l’EDA (Explorative Data Analysis) si potrebbe dover applicare delle trasformazioni ai dati per renderli adatti alla modellazione. Ad esempio, potrebbero essere necessarie trasformazioni per:

• convertire caratteristiche qualitative in quantitative utilizzando variabili fittizie.
• gestire i dati mancanti, ad esempio eliminando le righe con valori mancanti o cercando di completarle.

Inoltre, l’EDA comprende l’utilizzo di statistiche descrittive e visualizzazioni per ottenere una comprensione iniziale dei dati. Questo può includere:

• il calcolo di statistiche di base come media, mediana, deviazione standard
• la creazione di grafici come istogrammi e grafici a dispersione per visualizzare la distribuzione dei dati e le relazioni tra le variabili.

Riduzione della dimensionalità tramite machine learning

Lossy o lose-less. La riduzione di dimensionalità è il processo di riduzione del numero di colonne in un set di dati, non del numero di righe. Questo è utile in due scenari principali:

• Apprendimento senza supervisione: quando si cercano schemi di gruppi di punti simili senza prevedere esplicitamente le colonne.
• Apprendimento supervisionato: quando si prevede una variabile di risposta ma l’analisi esplorativa dei dati non evidenzia schemi chiari nelle dimensioni che gli esseri umani possono contemplare.

Ci sono due modi principali per implementare la riduzione dimensionale:

• Selezione delle caratteristiche: scelta di un sottoinsieme delle caratteristiche originali più informative.
• Estrazione delle caratteristiche: creazione di nuove “super-colonne” combinando le caratteristiche originali, in genere utilizzando formule matematiche complesse.

Apprendimento non supervisionato

L'apprendimento non supervisionato accetta una serie di predittori e utilizza le relazioni tra di essi per attività come la riduzione della dimensionalità e il clustering.

• L’apprendimento supervisionato non richiede dati etichettati, ovvero dati di addestramento in cui gli esempi storici sono etichettati con la risposta corretta.
• Può trovare gruppi di punti dati che si comportano in modo simile che un essere umano potrebbe non notare.
  • Può essere un passaggio di pre-elaborazione per l’apprendimento supervisionato raggruppando i punti dati e quindi utilizzando tali cluster come risposta.
• E’ importante l’ispezione umana perché l’algoritmo di clustering non ha alcuna conoscenza del contesto del dominio del problema e può solo dire quali cluster ha trovato, non cosa significano.

Poiché i modelli non supervisionati non tentano di trovare una relazione tra i predittori e una risposta specifica, non vengono utilizzati per effettuare previsioni. I modelli non supervisionati vengono utilizzati per trovare organizzazione e rappresentazione precedentemente sconosciute nei dati.

• Può essere difficile determinare se un risultato è corretto!

L’apprendimento non supervisionato è appropriato nelle seguenti situazioni:

• Quando la variabile di risposta non è del tutto chiara.
• Per estrarre una struttura dai dati in cui tale struttura o modello non sembra esistere.
• Quando si utilizza un concetto non supervisionato chiamato estrazione di feature, che consiste nel creare nuove feature da quelle esistenti.

Ad esempio, l’analisi cluster può riconoscere che ogni cluster osservato tramite le osservazioni è simile agli altri ma diverso da ogni altro cluster.

Clustering

Il clustering è un insieme di modelli di machine learning senza supervisione che tenta di raggruppare i punti dei dati in cluster in base ai centroidi.

• L’obiettivo del clustering è migliorare l’interpretabilità di un set di dati suddividendo i dati in gruppi.
• Il clustering fornisce un livello di astrazione rispetto ai singoli punti di dati, estraendo e migliorando la struttura naturale dei dati.

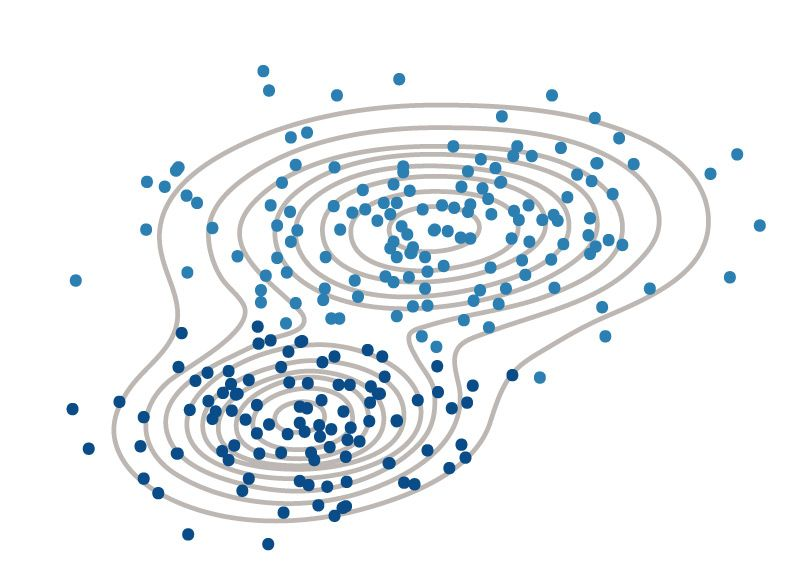
Definizioni:

• Cluster: un gruppo di punti dati che si comportano in modo simile.
• Centroide: il centro di un cluster. Può essere pensato come il punto medio del cluster.

Il concetto di somiglianza è fondamentale nella definizione di un cluster. Una maggiore somiglianza tra i punti porta a un clustering migliore.

• In molti casi, i dati vengono trasformati in punti in uno spazio n-dimensionale e la distanza tra questi punti viene utilizzata come forma di somiglianza.
• Il centroide del cluster è in genere la media di ogni dimensione (colonna) per ogni punto dati in ogni cluster.

Esistono molti tipi di procedure di clustering come il Clustering K-Means o il Clustering gerarchico. Esistono divere tecniche per stimare il numero ottimale di clusters come il metodo del gomito, misure di validazione interna, il silhouette score

Clustering K-Means

L’algoritmo K-means è un algoritmo di apprendimento non supervisionato spesso utilizzato per l’analisi dei gruppi partizionali.

• L’obiettivo principale è suddividere i dati in ‘K’ gruppi (omogenei) in modo che gli elementi facenti parte dello stesso cluster abbiano caratteristiche simili tra loro, e diverse rispetto agli elementi all’interno degli altri cluster.
  • Questo algoritmo fa in modo che ogni “oggetto” nella banca dati presa in analisi si trovi esattamente in un sottoinsieme (o cluster).
  • Utile per il riconoscimento di pattern e in ambito marketing.
• Adatto per analizzare ed elaborare grandi set di dati.
• Un algoritmo che risolve K-means in modo approssimato è l’Algoritmo di Lloyd.

Permette di suddividere un insieme di oggetti in ‘k’ gruppi in base alla somiglianza tra i loro attributi.

Il Clustering K-Means si svolge nei seguenti passaggi:

1. Fase di assegnazione: Posizionare casualmente dei centroidi iniziali nei dati e assegnare a ciascun punto al cluster rappresentato dal centroide più vicino.
2. Fase di aggiornamento: I centroidi vengono aggiornati calcolando la media di tutti i punti del cluster, successivamente (se necessario) si ripete il processo di riassegnazione del cluster più vicino.

• Il ciclo di assegnazione e aggiornamento dei centroidi si ripete (passaggi 1 e 2) fino a quando non si raggiunge una convergenza, cioè quando i centroidi non cambiano più o cambiano in modo minimo.

Come scegliere il numero ottimale di cluster?

Un aspetto cruciale del clustering K-means è determinare il numero ottimale di cluster (k). Il numero di cluster scelto influenza significativamente l’interpretazione dei dati e l’efficiacia del clustering stesso. Esistono diverse tecniche per stimare il numero ottimale di cluster, tra cui:

• le misure di validazione interna,
• il metodo del gomito
• il coefficiente di silhouette che è una metrica comunemente utilizzata nei casi in cui la disposizione del cluster non è nota.

Svantaggi

• K-Means può essere influenzato dalla scelta iniziale dei centroidi e dalla presenza di outliers nei dati, altri svantaggi possono scaturire dalla diversa natura dei clusters, in particolar modo
• I cluster possono nascondere una diversa natura l’uno dall’altro (diversa densità) adottando forme non globulari.
• Clusters di diverse dimensioni possono creare problemi in quanto l’algoritmo potrebbe privilegiare i cluster più grandi, trascurando i cluster più piccoli e meno popolati.
• Il numero di cluster deve essere fissato a priori
• E’ possibile adoperare l’algoritmo solo su dati vettoriali numerici (in quanto è necessario il calcolo della media).

Maledizione della dimensionalità

La maledizione della dimensionalità nel K-Means è che con l’aumentare del numero di feature (colonne) in un set di dati, è necessario un numero esponenzialmente maggiore di righe (punti dati) per riempire gli spazi vuoti creati dalle dimensioni aggiuntive. Questo perché, con l’aggiunta di più colonne, il numero finito di punti che abbiamo fatica a rimanere vicino, il che rende difficile per l’algoritmo K-Means raggruppare i dati in modo efficace.

La soluzione: La maledizione della dimensionalità può essere risolta aggiungendo più punti dati o implementando la riduzione della dimensionalità.

• La riduzione della dimensionalità riduce il numero di colonne in un set di dati senza ridurre il numero di righe.
  • Ciò può essere ottenuto con metodi come l’eliminazione delle feature o l’estrazione delle feature. L’eliminazione delle feature elimina semplicemente le feature che non sono rilevanti per il compito da svolgere, mentre l’estrazione delle feature utilizza formule matematiche per creare nuove “super-colonne” che sono una combinazione delle feature originali.

Clustering gerachico

Il clustering gerarchico è un metodo di analisi dati utilizzato per raggruppare insiemi di dati simili in categorie o cluster in modo gerarchico. In questo algoritmo, la distanza tra tutti i punti dati viene prima calcolata e i due punti più vicini vengono uniti. Questo processo viene ripetuto, con i punti dati e i cluster appena uniti fusi fino a quando non rimane un solo cluster. Un dendrogramma può essere utilizzato per visualizzare questo processo, con la lunghezza dei rami dell’albero del dendrogramma direttamente correlata alla distanza tra i punti uniti.

• Il clustering gerarchico è spesso utilizzato nell’analisi dei dati non supervisionata per ottenere una visione generale della struttura dei dati e identificare eventuali pattern o relazioni nello stesso.
• Il dendrogramma è un diagramma ad albero che rappresenta la gerarchia dei cluster e le relazioni di similarità tra di essi.
• Gli algoritmi di clustering gerarchico sono suddivisi in agglomerativi e divisivi.

Questa visualizzazione è utile per interpretare i risultati del clustering e per identificare i livelli di similarità tra i diversi cluster. Inoltre, il clustering gerarchico (agglomerativo o divisivo) può essere utilizzato per identificare cluster di diversi livelli di dettaglio.

Clustering gerarchico agglomerativo

Il clustering gerarchico agglomerativo è un metodo di clustering bottom-up in cui si parte dall'inserimento di ciascun elemento in un cluster differente e si procede quindi all'accorpamento graduale di cluster due a due. Il clustering gerarchico divisivo inizia con un unico cluster che comprende tutti i campioni e suddivide iterativamente il cluster in cluster più piccoli fino a quando ogni cluster non contiene un solo campione. Il clustering gerarchico agglomerativo, d’altra parte, inizia con ogni campione come un singolo cluster e unisce le coppie di cluster più vicine fino a quando non rimane un solo cluster.

1. Il processo inizia con ogni punto dati come singolo cluster.
2. I cluster vengono quindi uniti in coppie per creare una gerarchia di cluster.
3. La distanza euclidea può essere utilizzata per calcolare la distanza tra i punti dati.
4. I punti con la distanza più breve vengono uniti per primi e il processo continua fino a quando tutti i dati non sono stati uniti in un unico grande cluster.
5. La lunghezza dei rami nell’albero del dendrogramma risultante è correlata alla distanza tra i punti uniti.

Clustering gerarchico divisivo

Il clustering gerarchico divisivo è un metodo di clustering top-down in cui tutti gli elementi si trovano inizialmente in un singolo cluster che viene via via suddiviso ricorsivamente in un sotto-cluster.

1. Nel clustering gerarchico divisivo, tutte le osservazioni x j sono inizialmente parte di un unico grande cluster.
2. I dati vengono quindi suddivisi ricorsivamente in cluster sempre più piccoli.
3. La suddivisione continua fino a quando l’algoritmo non si ferma in base a un obiettivo specificato dall’utente.
4. Il metodo divisivo può suddividere i dati fino a quando ogni punto dati non è un nodo a sé stante.

Clustering gerarchico agglomerativo

Gli algoritmi di clustering gerarchico agglomerativo standard sono single linkage e complete linkage. Single linkage calcola le distanze tra i membri più simili per ogni coppia di cluster e unisce i due cluster per i quali la distanza tra i membri più simili è la più piccola. Complete linkage è simile a single linkage; tuttavia, invece di confrontare i membri più simili in ogni coppia di cluster, confronta i membri più dissimili per eseguire l’unione. Altri algoritmi comunemente usati per il clustering gerarchico agglomerativo includono average linkage e il collegamento di Ward. In average linkage, le coppie di cluster vengono unite in base alle distanze medie minime tra tutti i membri del gruppo nei due cluster. Nel metodo di Ward, i due cluster che portano al minimo aumento dell’SSE totale all’interno del cluster vengono uniti.

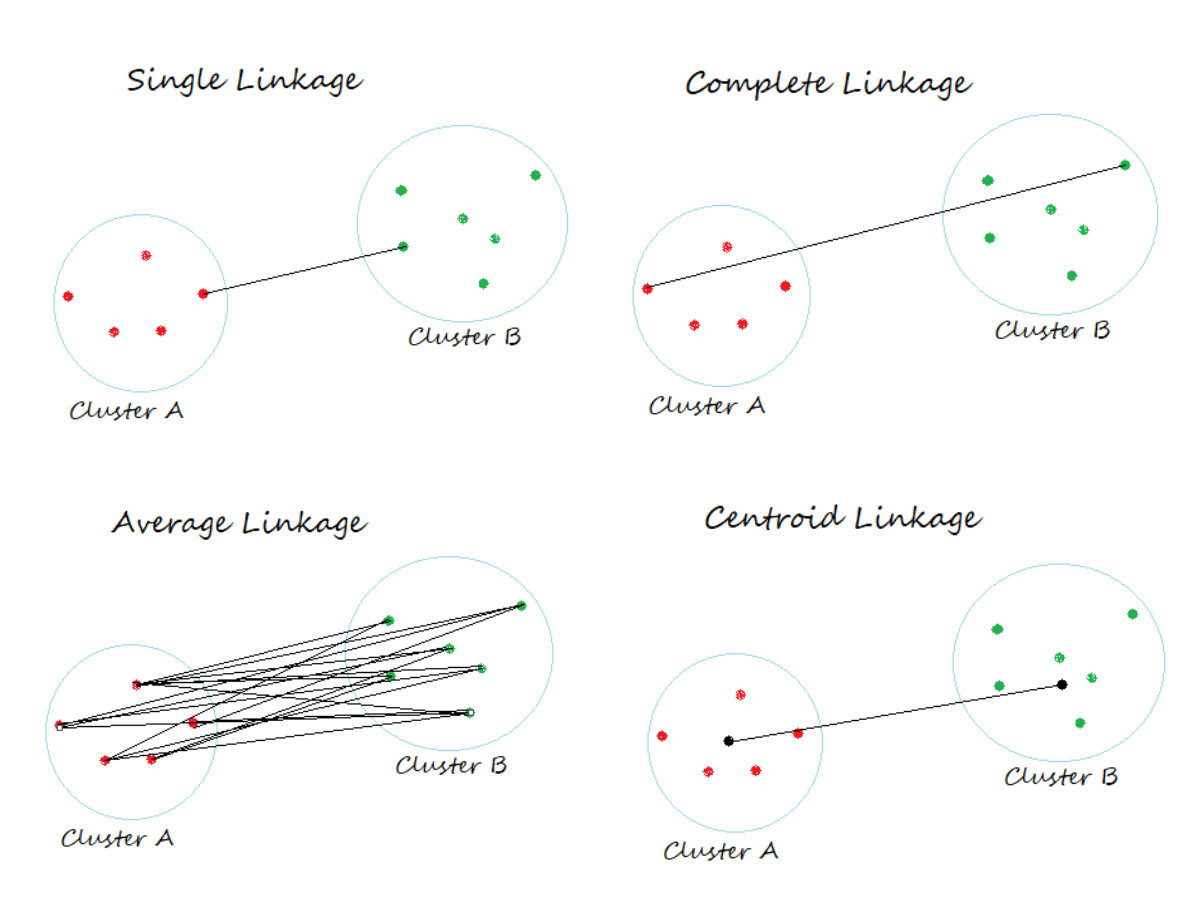
Il clustering gerarchico agglomerativo è un algoritmo di apprendimento non supervisionato che raggruppa i punti dati in cluster in base a una gerarchia. Questo approccio gerarchico può aiutare a visualizzare se i dati sono raggruppati, senza etichettatura o supervisione. L’output del clustering gerarchico è in genere presentato in un dendrogramma. Il clustering gerarchico agglomerativo è un approccio “bottom-up”. Inizia con ogni punto dati come un singolo cluster e poi unisce iterativamente le coppie di cluster più vicine finché non rimane un solo cluster. Il processo di unione dei dati alla fine si ferma quando tutti i dati sono stati uniti in un unico “uber cluster”. Il clustering gerarchico agglomerativo usa tipicamente una qualche forma di metrica di distanza per determinare la similarità tra i cluster. Alcune metriche di distanza tipiche includono:

• Distanza euclidea
• Distanza euclidea al quadrato
• Distanza di Manhattan
• Distanza massima
• Distanza di Mahalanobis

L’algoritmo del dendrogramma è il seguente:

1. Calcolare la distanza tra tutti gli punti dati .
2. Unire i due punti dati più vicini in un unico nuovo punto dati a metà strada tra le loro posizioni originali.
3. Ripetere il calcolo con i nuovi punti.

L’algoritmo continua finché i dati non sono stati uniti gerarchicamente in un unico punto dati. La lunghezza dei rami dell’albero del dendrogramma è direttamente correlata alla distanza tra i punti uniti. Il comando “threshold” è importante per etichettare dove ogni punto appartiene nello schema gerarchico. Impostando la soglia a livelli diversi, ci possono essere più o meno cluster nel dendrogramma.

Il clustering gerarchico agglomerativo ha diversi vantaggi rispetto ad altri algoritmi di clustering, come il clustering k-means:

• Non è necessario specificare in anticipo il numero di cluster.
• Può essere utilizzato per creare raggruppamenti significativi.
• I risultati possono essere visualizzati in un dendrogramma, che può aiutare nell’interpretazione dei risultati.

Tuttavia, il clustering gerarchico agglomerativo può anche essere computazionalmente costoso, soprattutto per grandi set di dati.

Valutazione qualità clustering

Misure di validazione interna

Le misure di validazione interna valutano la qualità del clustering per diversi valori di k, senza richiedere informazioni esterne come le etichette di classe preesistenti.

• Una misura comune è la somma totale entro il cluster di square (WSS), che rappresenta la distanza media tra ciascun punto dati e il centroide del suo cluster assegnato.
  • Un valore di WSS inferiore indica un clustering più compatto e, di conseguenza, un numero di cluster più appropriato.

Metodo del gomito

Il metodo del "gomito" è una tecnica visiva per identificare il numero ottimale di cluster basandosi sul WSS. Il ragionamento dietro al metodo del “gomito” è che, aggiungendo più cluster, il WSS tende a diminuire inizialmente in modo significativo, poiché i punti dati vengono raggruppati in modo più efficiente. Tuttavia, dopo un certo punto, la riduzione del WSS diventa minima, suggerendo che l’aggiunta di ulteriori cluster non migliora significativamente la qualità del clustering. Il “gomito” rappresenta il punto in cui la riduzione del WSS diventa marginale, indicando che il numero di cluster associato a quel punto è il più appropriato

Il metodo del “gomito” funziona come segue:

1. Eseguire l’algoritmo di clustering per diversi valori di k, ad esempio da 1 a 10. 2. Per ogni valore di k, calcolare il WSS. 3. Creare un grafico con il numero di cluster sull’asse x e il WSS sull’asse y.
2. Osservare la forma del grafico: il punto in cui la curva si appiattisce bruscamente, formando un “gomito”, indica il numero ottimale di cluster.

Coefficiente silhouette

Il coefficiente di silhouette è una metrica utilizzata per valutare la qualità di un clustering, misurando la coesione all’interno dei cluster e la separazione tra cluster. A differenza del metodo del “gomito”, che si concentra sulla valutazione globale del clustering basandosi sulla somma totale entro il cluster di square (WSS), il coefficiente di silhouette fornisce informazioni sulla qualità del clustering a livello di singolo punto e di cluster.

Calcolo del coefficiente di silhouette: Per ogni punto dati i nel dataset:

1. Calcolare la distanza media tra il punto e tutti gli altri punti dati nel suo cluster assegnato.
2. Calcolare la distanza media tra il punto dai punti dati di un cluster diverso.
3. Il coefficiente di silhouette per il punto è definito come: se (o se )

Interpretazione del coefficiente di silhouette:

• Valori alti (vicini a 1): Il punto è ben posizionato all’interno del suo cluster e lontano da altri cluster. Questo indica un clustering di buona qualità.
• Valori bassi (vicini a 0): Il punto si trova sul confine tra due cluster o è rumore. Questo indica un clustering di qualità inferiore.
• Valori negativi: Il punto è meglio posizionato in un cluster diverso da quello a cui è stato assegnato. Questo indica un errore di clustering.

Coefficiente di silhouette per un cluster: Il coefficiente di silhouette può essere calcolato anche per un intero cluster, come media dei coefficienti di silhouette di tutti i punti dati appartenenti a quel cluster. Un valore medio alto per un cluster indica che i punti dati all’interno del cluster sono ben raggruppati e coesi.

Coefficiente di silhouette per l’intero clustering: Il coefficiente di silhouette può essere calcolato anche per l’intero clustering, come media dei coefficienti di silhouette di tutti i punti dati nel dataset. Un valore medio alto per l’intero clustering indica che il clustering è di buona qualità in generale, con la maggior parte dei punti dati ben posizionati all’interno dei loro cluster e con una buona separazione tra cluster.

Confronto con il metodo del “gomito”: Il metodo del “gomito” e il coefficiente di silhouette sono entrambi utilizzati per valutare la qualità del clustering, ma si basano su approcci differenti. Il metodo del “gomito” si concentra sulla riduzione del WSS all’aumentare del numero di cluster, mentre il coefficiente di silhouette valuta la coesione all’interno dei cluster e la separazione tra cluster a livello di singolo punto e di cluster.

• Il metodo del “gomito” è un metodo visivo semplice da interpretare, ma può essere influenzato dalla scelta della metrica di distanza e non fornisce informazioni sulla qualità di ogni punto dati individualmente. Il coefficiente di silhouette, invece, offre informazioni più dettagliate sulla qualità del clustering a diversi livelli, ma il suo calcolo può essere più complesso e la sua interpretazione può essere meno immediata.

Apprendimento supervisionato

L'apprendimento supervisionato trova le associazioni tra le caratteristiche di un set di dati e una variabile target.

• L’apprendimento supervisionato richiede dati etichettati, ovvero dati di addestramento in cui gli esempi storici sono etichettati con la risposta corretta.
• L’obiettivo è trovare una relazione tra predittori e risposta per fare una previsione.
  • Questi modelli sono spesso chiamati modelli di analisi predittiva perché possono fare previsioni basate su esempi passati.

Esempio: Ad esempio, un modello di apprendimento supervisionato potrebbe essere utilizzato per trovare l’associazione tra i segni vitali di una persona, come la frequenza cardiaca o il livello di obesità, e la probabilità che quella persona abbia un attacco di cuore.

Altri esempi di utilizzo di un modello di apprendimento supervisionato potrebbero essere:

• Prevedere il mercato azionario,
• le previsioni meteorologiche,
• previsioni sulla criminalità.

I due tipi di modelli di apprendimento supervisionato sono regressione e classificazione.

La Regressione lineare

Ad esempio, in biologia, un modello spawner/reclute viene utilizzato per valutare la salute di una specie analizzando la relazione tra il numero di unità parentali sane in una specie e il numero di nuove unità nel gruppo di animali.8 La creazione di un modello per questi dati può consentire ai ricercatori di prevedere il numero di nuove unità prodotte da un gruppo di spawners o di stimare il numero di spawners necessari per produrre un certo numero di reclute.8 Tuttavia, è importante notare che solo perché esiste una correlazione matematica tra le variabili, non significa che esista una relazione di causa ed effetto tra loro.10 Potrebbero esserci fattori di confondimento in gioco o potrebbero non avere nulla a che fare tra loro.10 La correlazione non implica la causalità.

La regressione multipla

La regressione multipla è un processo statistico che utilizza diverse variabili esplicative per prevedere il risultato di una variabile di risposta. Questo processo è utile per la modellazione della relazione tra variabili in un set di dati. L’obiettivo della regressione multipla è trovare un modello che descriva meglio la relazione tra le variabili esplicative e la variabile di risposta. La regressione multipla è una versione più generale della regressione lineare semplice, che utilizza solo una variabile esplicativa.

La discesa di un gradiente

La discesa del gradiente è un algoritmo di ottimizzazione usato per trovare il minimo di una funzione. TensorFlow, una libreria di machine learning, usa la discesa del gradiente per minimizzare iterativamente una funzione di errore e adattare un modello ai dati. Questo processo prevede l’attraversamento iterativo dell’intero set di dati e l’aggiornamento progressivo del modello. La velocità di apprendimento, che non dovrebbe essere troppo vicina a 0, influenza la velocità con cui il modello apprende dai dati. Una velocità di apprendimento più lenta è generalmente preferibile per consentire al modello di convergere alla risposta corretta.

La discesa del gradiente può essere concettualizzata come scendere da una collina fino a raggiungere un minimo locale o globale. Ad ogni iterazione, l’algoritmo fa un passo lontano dal gradiente, determinato dalla dimensione del passo e dalla pendenza del gradiente. La dimensione del passo è influenzata dal valore della velocità di apprendimento e dalla pendenza del gradiente.

Nell’ambito delle reti neurali, la discesa del gradiente svolge un ruolo cruciale nell’addestramento della rete. Viene utilizzata per aggiornare i pesi della rete minimizzando la funzione di errore. Il processo di backpropagation, che implica il calcolo dei gradienti della funzione di errore rispetto ai pesi della rete, consente di propagare l’errore all’indietro attraverso la rete. Questa retropropagazione consente di aggiornare i pesi in modo iterativo utilizzando la regola di aggiornamento della discesa del gradiente. L’ottimizzazione della dimensione del passo iterativo è essenziale per la convergenza dell’algoritmo di discesa del gradiente. Tecniche come fminsearch possono essere impiegate per determinare il valore appropriato della dimensione del passo.

Overfitting e Underfitting nell’apprendimento supervisionato

Nell’apprendimento supervisionato, l’overfitting si verifica quando un modello si adatta eccessivamente al set di dati di addestramento, imparando non solo le tendenze generali, ma anche il rumore o le peculiarità specifiche di quei dati. Di conseguenza, il modello mostrerà un’elevata accuratezza sui dati di addestramento (basso bias), ma avrà difficoltà a generalizzare a nuovi dati non visti prima (alta varianza). In pratica, l’overfitting porta a modelli che funzionano molto bene sui dati su cui sono stati addestrati, ma che falliscono nel prevedere accuratamente su dati nuovi.

Al contrario, l’underfitting si verifica quando un modello è troppo semplice per catturare le relazioni complesse presenti nei dati. Questo si traduce in un modello che non si adatta bene né ai dati di addestramento né a quelli di test, risultando in un’accuratezza predittiva scarsa in entrambi i casi (alto bias e bassa varianza). In pratica, l’underfitting porta a modelli che non riescono a catturare le informazioni importanti presenti nei dati, limitando la loro capacità di generalizzare.

L’obiettivo dell’apprendimento supervisionato è quello di trovare un equilibrio tra overfitting e underfitting, creando un modello che generalizzi bene a nuovi dati. Questo equilibrio si ottiene tipicamente attraverso tecniche come la convalida incrociata, la regolarizzazione e la scelta del modello appropriato.

Il classificatore Bayesiano

Un Classificatore Bayesiano Naïve è un modello di classificazione di machine learning che utilizza il Teorema di Bayes per classificare i punti dati.

• Un classificatore bayesiano naif presuppone che ciascuna caratteristica sia indipendente da tutte le altre caratteristiche.
• Il modello richiede dati etichettati con n caratteristiche (x1, x2, …, xn) e un’etichetta di classe, C.
  • Ad esempio, quando si classificano messaggi di testo come spam, le caratteristiche sarebbero le parole e le frasi nel messaggio di testo e l’etichetta di classe sarebbe “spam” o “ham”.

Il classificatore K-Nearest Keighbors (KNN)

L’algoritmo K-Nearest Neighbors è un algoritmo di apprendimento supervisionato che utilizza un paradigma di somiglianza, ovvero effettua previsioni sulla base di punti di dati simili, che ha già incontrato in passato.

• L’algoritmo KNN accetta in input la complessità, K, che rappresenta con quanti punti di dati simili eseguire il confronto. Se K = 3, allora, per un dato input, cerchiamo i tre punti di dati più vicini e li usiamo per la nostra previsione.
• In questo caso, K è la complessità del nostro modello.

Analisi del componente principale (PCA)

L'analisi delle componenti principali (PCA) è una tecnica di trasformazione lineare non supervisionata utilizzata per la riduzione della dimensionalità.

• La tecnica permette di trovare le componenti principali all’interno di un sistema di variabili correlate, aiuta quindi ad identificare i modelli nei dati in base alla correlazione tra le caratteristiche. L’analisi PCA è un modello di estrazione delle caratteristiche.
  • Ha lo scopo di ridurre il numero di variabili che descrivono un insieme di dati a un numero minore di variabili latenti, limitando il più possibile la perdita di informazioni.
    • Crea un numero specificato di nuove “super-colonne” per rappresentare i dati originali con meno colonne.
• La PCA mira a trovare le direzioni della varianza massima nei dati ad alta dimensionalità e a proiettarli su un nuovo sottospazio con dimensioni uguali o inferiori a quello originale.
  • Questo permette di individuare pattern nascosti e di comprendere meglio le relazioni tra le variabili.
• La PCA può essere utilizzata anche per l’analisi esplorativa dei dati e la rimozione del rumore dai segnali.

L’analisi delle componenti principali (PCA, anche nota come trasformata di Karhunen-Loève) è la principale tecnica lineare per la riduzione della dimensionalità.

La PCA segue i seguenti step:

1. Standardizzazione dati.
2. Calcolo della matrice di covarianza per identificare correlazioni.
3. Calcolo degli autovalori e autovettori della matrice di covarianza per identificare le componenti principali
4. Creare un vettore di features per decidere quali componenti principali mantenere.
   • È importante valutare attentamente quali componenti mantenere per evitare sovrapposizioni e garantire la conservazione delle informazioni essenziali.
5. Riformulare i dati lungo gli assi delle componenti principali
   • Per ottenere questo risultato, i dati originali standardizzati devono essere moltiplicati per la matrice degli autovettori delle componenti principali selezionate.

Vantaggi:

• Elaborazione del modello più rapida
• Possibile miglioramento delle prestazioni predittive
• Possibilità di ottenere maggiori conoscenze dalle caratteristiche estratte

Svantaggi:

• Perdita di interpretabilità delle caratteristiche, poiché si opera con colonne di derivazione matematica
• Possibile perdita di prestazioni predittive a causa della riduzione delle informazioni

Standardizzazione dati

La standardizzazione dati è utile per analizzare equamente il contributo di ciascuna variabile.

• Per standardizzare, bisogna sottrarre la media da ogni valore di variabile e dividere per la deviazione standard corrispondente.
• Dopo aver standardizzato i dati, è possibile calcolare la matrice di covarianza per analizzare le relazioni tra le variabili.
  • La matrice quadrata riporta la varianza e la covarianza delle variabili del dataset, fondamentali per l’analisi delle componenti principali.

La deviazione standard

La deviazione standard è un concetto utilizzato nella statistica per descrivere la dispersione dei dati rispetto alla media aritmetica. In sostanza, la deviazione standard misura la distanza media tra i valori di un set di dati e la loro media.

Calcolo della deviazione standard:

1. Calcolare la media dei dati.
2. Sottrarre la media da ciascun valore nel set di dati ed elevare al quadrato il risultato.
3. Calcolare la media di tutte le differenze al quadrato (questo valore è chiamato varianza).
4. Calcolare la radice quadrata della varianza. Il risultato è la deviazione standard.

Calcolo degli autovalori e autovettori

In seguito, si procede al calcolo degli autovalori e degli autovettori della matrice di covarianza.

• Gli autovettori indicano le direzioni delle nuove dimensioni (componenti principali).
• Gli autovalori indicano l’importanza di ciascuna di queste direzioni.

Cosa cambia tra una PCA ed un'altra?

Le componenti principali sono organizzate in base alla loro importanza, con la componente iniziale catturante la maggiore variazione nei dati e le successive componenti che catturano variazioni minori.

• Le componenti sono ortogonali tra loro, ossia non dipendenti e senza nessuna correlazione.

Score e loadings

Gli score e i loadings rappresentano uno degli aspetti fondamentali del PCA.

• Gli score rappresentano le coordinate dei dati originali proiettati sulle componenti principali aggiornate.
  • Gli score rappresentano la distribuzione dei dati all’interno delle nuove dimensioni individuate dalle componenti principali.
• I loadings rappresentano i coefficienti che mostrano quanto ogni variabile originale contribuisca a ciascuna componente principale.
  • Con i loadings è possibile interpretare le componenti principali in relazione alle variabili originali, offrendo un’idea chiara dell’influenza di ogni singola variabile sulle nuove dimensioni.

Decomposizione ai Valori Singolari (SVD)

La Decomposizione ai Valori Singolari (SVD) è una tecnica di riduzione dati che consiste nella fattorizzazione di matrici di fondamentale importanza nell’ambito della scienza computazionale e dell’ingegneria. La SVD può essere vista come un metodo per trovare una base di dati “su misura”, a differenza della Trasformata Veloce di Fourier (FFT) che fornisce una base generica.

Utilità e Proprietà:

• Riduzione della Dimensionalità: La SVD consente di approssimare una matrice di dati di grandi dimensioni con una versione di rango inferiore, mantenendo le informazioni più significative. Questa approssimazione, detta SVD troncata, si ottiene selezionando un numero limitato di valori singolari dominanti.
• Pseudoinversa: La SVD è utile per calcolare la pseudoinversa di matrici non quadrate, consentendo di trovare soluzioni ai minimi quadrati per sistemi di equazioni lineari anche quando non esiste una soluzione esatta.
• Denoising dei dati: La SVD può essere utilizzata per ridurre il rumore nei set di dati, sfruttando il fatto che i valori singolari più piccoli spesso corrispondono a componenti di rumore.
• Analisi delle Correlazioni: La SVD è alla base dell’Analisi delle Componenti Principali (PCA), un metodo per trovare le direzioni di massima varianza (componenti principali) nei dati.
• Applicazioni Dinamiche: La SVD è utilizzata in diversi metodi per l’analisi di sistemi dinamici, tra cui la Decomposizione Modale Dinamica (DMD) e la Decomposizione Ortogonale Propria (POD). Questi metodi scompongono i dati in “modi” che rappresentano strutture coerenti nello spazio e nel tempo.

Implementazione e Ottimizzazione:

• La scelta del numero di valori singolari da mantenere (troncamento) è cruciale e dipende da fattori come la varianza da catturare e il livello di rumore nei dati.

Limitazioni:

• La SVD è sensibile all’allineamento dei dati. Traslazioni, rotazioni o ridimensionamenti possono influenzare significativamente i valori singolari e i vettori singolari risultanti.
• La SVD standard non gestisce in modo ottimale le invarianze nei dati, come quelle derivanti da traslazioni o rotazioni. Esistono tecniche specifiche per affrontare queste situazioni, come l’utilizzo di informazioni sulle simmetrie del problema.

Pseudoinversa

La pseudoinversa generalizza l’inversa di una matrice per matrici non quadrate ed è spesso usata per calcolare la soluzione ai minimi quadrati di un sistema di equazioni.

La Decomposizione ai Valori Singolari (SVD) è un metodo comune per calcolare la pseudoinversa: data la SVD X = UΣV†, la pseudoinversa è X† = VΣ^−1 U†. U, le cui colonne sono autovettori sinistri di X, è generalmente una matrice quadrata unitaria. Pertanto, U∗U = UU∗ = In×n. Tuttavia, per calcolare la pseudoinversa di X, è necessario calcolare X† = ṼΣ̃−1Ũ∗ poiché solo Σ̃ è invertibile (se tutti i valori singolari sono diversi da zero). Σ, in generale, non è invertibile. Infatti, generalmente non è nemmeno quadrata.

La pseudoinversa è utile nell’ambito dell’apprendimento automatico, ad esempio per calcolare soluzioni per sistemi sovradeterminati e sottodeterminati. Ad esempio, nel caso di un sistema sovradeterminato in cui non esiste una soluzione, è spesso utile trovare la soluzione x che minimizza l’errore quadratico medio ‖Ax− b‖22, la cosiddetta soluzione ai minimi quadrati.

La pseudoinversa può essere calcolata efficientemente dopo aver calcolato la SVD. Invertire le matrici unitarie Ũ e Ṽ comporta la moltiplicazione di matrici per le matrici trasposte, che richiede operazioni O(n2). Invertire Σ̃ è ancora più efficiente poiché è una matrice diagonale e richiede operazioni O(n). Al contrario, invertire una matrice quadrata densa richiederebbe un’operazione O(n3).

Pipeline data processing

Le pipeline semplificano i flussi di lavoro di machine learning consentendo di adattare un modello includendo un numero arbitrario di passaggi di trasformazione e applicarlo per fare previsioni su nuovi dati. Ad esempio, una pipeline potrebbe includere due passaggi intermedi: un trasformatore StandardScaler e un trasformatore PCA, nonché un classificatore di regressione logistica come stimatore finale. Quando viene eseguito il metodo di adattamento sulla pipeline, StandardScaler esegue l’adattamento e la trasformazione sui dati di addestramento e i dati di addestramento trasformati vengono quindi passati all’oggetto successivo nella pipeline, il PCA. Analogamente al passaggio precedente, PCA esegue anche l’adattamento e la trasformazione sui dati di input ridimensionati e li passa all’elemento finale della pipeline, lo stimatore.

• Non esiste un limite al numero di passaggi intermedi in questa pipeline.
• In sostanza l’informazione passa attraverso tutti i compartimenti, ognuno di essi restituisce un output che è dato in input al successivo e così finché la pipeline viene completata.

Questa struttura di processamento dati consente di avere un flusso costante di informazioni nei vari compartimenti della pipeline.

Riconosciamo 3 step chiave:

1. Data collection
2. Processamento
3. Destinazione

Stimatore

Uno stimatore (o stima puntuale) è una funzione che associa ad ogni campione un valore del parametro da stimare.

• Il valore assunto dallo stimatore in corrispondenza ad un particolare campione è detto stima.

Varianza

La varianza di una variabile casuale rappresenta la dispersione della variabile. Quantifica la variabilità del valore atteso. In altre parole, la varianza misura quanto i valori di un set di dati sono “sparsi” rispetto alla media. Per una variabile casuale discreta, la varianza è calcolata con la seguente formula: Varianza = V[X] = σX2 = Σ (xi - μX)2 pi

Dove:

• xi è l’i-esimo risultato
• pi è l’i-esima probabilità
• μx rappresenta il valore atteso della variabile

La deviazione standard, indicata con σX, è semplicemente la radice quadrata della varianza.

Esempi di Varianza in Azione

• Esempio 1: Valutazione di un progetto Supponiamo che un direttore stia valutando il successo di un nuovo prodotto su una scala da 0 a 4. Utilizzando la distribuzione di probabilità, il valore atteso di successo del prodotto (μX) è 2.81. Calcolando la varianza (σX2) si ottiene un valore di 0.93, che si traduce in una deviazione standard (σX) di circa 0.96.

  Questo significa che il direttore può aspettarsi che il progetto abbia un punteggio di successo di 2.81, più o meno 0.96, ovvero tra 1.85 e 3.77. In altre parole, il progetto avrà probabilmente un punteggio di successo di 2.81, più o meno un punto.

• Esempio 2: Numero di amici di Facebook Se si raccoglie un campione casuale di 24 persone e si registra il loro numero di amici di Facebook, si può calcolare la deviazione standard (s) per misurare la dispersione dei dati. Utilizzando la formula della deviazione standard o un programma Python, si ottiene una deviazione standard di 425.2 amici di Facebook.

  Questo numero (425.2) rappresenta la dispersione dei dati e può essere interpretato come una sorta di distanza media tra i valori nei dati e la media.

Utilizzo della Varianza in Scienza dei Dati

In scienza dei dati, la varianza è una metrica cruciale per valutare i modelli di apprendimento automatico, in particolare quando si esaminano i compromessi tra bias e varianza.

• Bias: Misura l’accuratezza di un modello, ovvero quanto le previsioni del modello sono vicine ai valori reali. Un modello con basso bias fa previsioni accurate in media.

• Varianza: Misura la sensibilità di un modello alle variazioni nei dati di addestramento. Un modello con bassa varianza produce previsioni simili anche quando viene addestrato su diversi set di dati provenienti dalla stessa popolazione.

L’obiettivo è quello di trovare un equilibrio tra bias e varianza, cercando di ottenere sia un basso bias che una bassa varianza. Tuttavia, spesso è necessario un compromesso: modelli più complessi possono avere un bias inferiore ma una varianza maggiore (overfitting), mentre modelli più semplici possono avere una varianza inferiore ma un bias maggiore (underfitting). La convalida incrociata è una tecnica utilizzata per valutare e mitigare i problemi di bias e varianza, aiutando a selezionare il modello con le migliori prestazioni predittive.

Predittore

Un predittore in questo contesto può essere inteso come una variabile o una caratteristica di un set di dati che viene utilizzata per prevedere o stimare il valore di un’altra variabile, chiamata variabile di risposta. In altre parole, un predittore è un’informazione che ci aiuta a fare previsioni su un determinato fenomeno o evento.

Esempi di Predittori

• Nel caso di un modello di machine learning che cerca di prevedere il rischio di un attacco cardiaco, i predittori potrebbero essere variabili come il colesterolo, la pressione sanguigna, l’altezza, il fumo e altre informazioni mediche del paziente.
• In un modello che mira a prevedere se un cliente acquisterà un determinato prodotto, i predittori potrebbero essere l’età, il sesso e lo stato lavorativo del cliente.
• In un modello che analizza le recensioni dei ristoranti, le parole utilizzate nella recensione possono essere considerate predittori per determinare se la valutazione sarà di 5 o 1 stella.

Relazione tra Predittori e Variabile di Risposta

I modelli di machine learning cercano di individuare relazioni tra i predittori e la variabile di risposta. Queste relazioni possono essere utilizzate per fare previsioni su nuove osservazioni o per comprendere meglio come i predittori influenzano la variabile di risposta. È importante sottolineare che la presenza di una correlazione tra un predittore e la variabile di risposta non implica necessariamente una relazione di causalità.

Importanza dei Predittori

Non tutti i predittori sono ugualmente importanti per fare previsioni accurate. Alcuni predittori potrebbero avere un impatto maggiore sulla variabile di risposta rispetto ad altri. Ad esempio, nell’esempio del modello che prevede gli ingaggi dei giocatori di baseball, il numero di anni di attività del giocatore nel campionato è risultato essere il predittore più importante. La selezione delle caratteristiche è un aspetto cruciale del machine learning, in cui si cerca di identificare i predittori più rilevanti per un determinato problema.

Stimatore

Lo stimatore è una funzione su un campione di dati che cerca di stimare alcune qualità, utili a. In sostanza, quando non è possibile raccogliere informazioni da un’intera popolazione (ad esempio, tutti i dipendenti di un’azienda o tutti i fumatori del mondo), si seleziona un sottoinsieme di quella popolazione, chiamato campione, e si usa quel campione per “stimare” una caratteristica della popolazione più ampia. La stima del punto è il singolo valore calcolato dal campione che rappresenta la nostra migliore ipotesi sul valore reale del parametro nella popolazione più ampia.

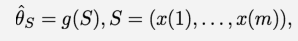
Ad esempio, se vogliamo conoscere la durata media delle pause dei dipendenti in un’azienda di 9.000 persone, potremmo campionare 100 dipendenti e calcolare la durata media delle loro pause. Questa media campionaria sarebbe la nostra stima puntuale.

Le fonti evidenziano che le stime puntuali, sebbene utili, presentano dei limiti. Sono suscettibili agli errori derivanti da vari fattori, tra cui i pregiudizi di campionamento. Inoltre, l’ottenimento di più campioni per creare distribuzioni campionarie può essere poco pratico.

Anche se le fonti non forniscono una definizione specifica di “stimatore”, si può dedurre che, dato il contesto di una “stima puntuale” come stima di un parametro della popolazione, uno stimatore potrebbe riferirsi alla formula o al metodo specifico utilizzato per calcolare la stima puntuale dai dati campionari.

Media campionaria

Ad esempio, la media campionaria è uno stimatore comune per la media della popolazione. Tuttavia, senza ulteriori informazioni dalle fonti, questa è una deduzione e potrebbe essere necessaria una verifica indipendente per confermare se “stimatore” si riferisce effettivamente alla formula o al metodo utilizzato per calcolare una stima puntuale.

Distribuzione di Poisson

La Distribuzione di Poisson (o poissoniana) è una distribuzione di probabilità discreta che esprime la probabilità per il numero di eventi che si verificano successivamente e separatamente in un certo intervallo di tempo, mediamente se ne verificano un numero .

• Questa distribuzione è anche nota come legge degli eventi rari.

Distribuzione campionaria

E’ un tipo di

ESAMI

• DIFFERENZA TRA STIMATORE E VARIANZA
• DISTRIBUZIONI CANONICHE
• DISTRIBUZIONE BINOMIALE
• DISTRIBUZIONE UNIFORME
• LA FUNZIONE DI DENSITà DELLA PROBABILITà
• FUNZIONE DI DISTRIBUZIONE CUMULATIVA
• DISTRIBUZIONE DI POISSON
• DISTRIBUZIONE NORMALE/GAUSSIANA
• DISTRIBUZIONE CAMPIONARIA
• PREDITTORE
• BIAS-VARIANCE DECOMPOSITION