Grafo (Struttura dati)

Un grafo è una struttura dati che consiste in un insieme di elementi (nodi o vertici) collegati da linee (archi o spigoli). Possono essere orientati o non orientati, e pesati.

Grafo non orientato

Un grafo non orientato è un insieme di punti (nodi o vertici) e di linee (archi).

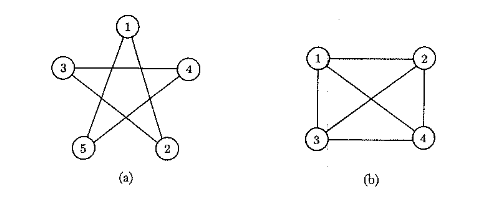
Il numero di archi ad un particolare nodo è il grado di tale nodo. Non è permesso più di un arco tra due nodi dati. E’ permessa l’esistenza di un arco da un nodo a se stesso, chiamato self-loop.

I grafi sono usati per la rappresentazione di dati. Per comodità assegniamo un’etichetta ai nodi e/o agli archi di un grafo.

Un cammino è una sequenza di nodi collegati da archi, riconosciamo:

• Cammino semplice: non contiene nodi ripetuti
• Cammino connesso: se per ogni coppia di nodi esiste un cammino tra di loro.

Un cammino è un ciclo se inizia e termina nello stesso nodo. Un ciclo semplice contiene almeno 3 nodi e ripete solo il primo e l’ultimo. Un grafo è un albero se è connesso e non ha cicli semplici, un albero può contenere un nodo speciale chiamato radice. I nodi di grado 1 in un albero, ad eccezione della radice, sono chiamati foglie.

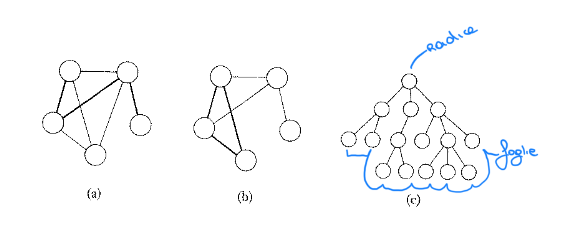(a) Un cammino in un grafo, (b) un ciclo in un grafo, (c) un albero

Grafo orientato

Un grafo orientato (o diretto) ha frecce (e non linee come nei grafi non orientati). Il numero delle frecce che escono da un nodo è il grado uscente di quel nodo ed il numero delle frecce che entrano in un nodo è il grado entrante.

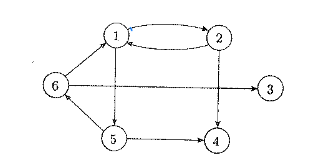
Un cammino in cui tutte le frecce sono orientate nella stessa direzione si definisce cammino orientato (o diretto):

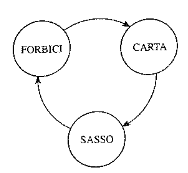
• Concetto:
  • Rappresentazioni:
    • Matrice di Adiacenza: Una matrice NxN dove N è il numero di vertici. a_ij = 1 se esiste un arco (i,j), 0 altrimenti. Per grafi pesati, a_ij = peso. Per grafi orientati, la matrice non è simmetrica.
    • Lista di Adiacenza: Un array Adj di N liste, una per ogni vertice. Adj[u] contiene tutti i vertici v tali che esista un arco (u,v).
  • Traversate:
    • Visita in Ampiezza (BFS - Breadth-First Search): Esplora il grafo livello per livello, trovando i cammini minimi in grafi non pesati. Utilizza una coda. Complessità O(V+E).
      • Sottografo dei Predecessori: Generato da BFS, un albero di visita in ampiezza che contiene i cammini minimi da una sorgente a ogni nodo raggiungibile.
    • Visita in Profondità (DFS - Depth-First Search): Esplora il grafo in profondità lungo ogni ramo prima di tornare indietro. Non usa una coda esplicita ma la ricorsione (stack implicito). Complessità O(V+E).
      • Foresta di Alberi di Visita: DFS produce una foresta di alberi che riflettono le chiamate ricorsive.
  • Problemi sui Grafi:
    • Alberi di Connessione Minima (Minimum Spanning Tree - MST): Trova un sottoinsieme di archi che connette tutti i vertici con il peso totale minimo.
      • Algoritmo di Kruskal: Algoritmo avido che aggiunge archi sicuri (di peso minimo) unendo alberi diversi fino a formare un MST. Utilizza una Struttura Dati per Insiemi Disgiunti (Disjoint Set Union - DSU).
        • DSU (implementata con liste concatenate): MakeSet(x) (crea un insieme con x), FindSet(x) (restituisce il rappresentante dell’insieme di x), Union(x,y) (unisce gli insiemi di x e y). Complessità per Kruskal: O(E lg E) o O(E lg V).
      • Algoritmo di Prim: Algoritmo avido che costruisce un MST espandendo un singolo albero a partire da una radice, aggiungendo l’arco leggero che connette l’albero a un vertice esterno. Utilizza una Coda a Min-Priorità. Complessità O(E lg V).
    • Cammini Minimi (Shortest Path): Trova il cammino con il peso minimo tra due vertici o da una sorgente a tutti gli altri.
      • Algoritmo di Bellman-Ford: Risolve il problema del cammino minimo da sorgente unica con pesi degli archi negativi. Rileva cicli negativi. Complessità O(VE).
      • Cammino Minimo su DAG (DAG Shortest Path): Per grafi orientati aciclici (DAG), è più efficiente. Si basa sull’ordinamento topologico e rilassamento degli archi. Complessità O(V+E).
      • Algoritmo di Dijkstra: Algoritmo avido per cammini minimi da sorgente unica su grafi con pesi degli archi non negativi. Utilizza una Coda a Min-Priorità. Complessità O(E lg V).
      • Relaxation: Operazione fondamentale (Relax(u,v,w)) che aggiorna la stima del cammino minimo a v se si trova un percorso migliore tramite u.
  • Esempio: Un sistema di navigazione GPS che trova il percorso più breve o veloce tra due punti su una mappa.