Terminologia, notazione matematica, grafi, logica Booleana, stringhe e linguaggi

in-corso

Insiemi

Per descrivere un insieme contenente elementi in base ad una qualche regola scriviamo: Per esempio questa notazione indica l’insieme dei quadrati perfetti:

• L’unione di A e B è l’insieme ottenuto combinando tutti gli elementi di A e B in un unico insieme:

• L’intersezione di A e B è l’insieme di tutti gli elementi che di A e B in un unico insieme:

• Il completamento di A è l’insieme di tutti gli elementi in esame che non sono in A.

Gli insiemi sono rappresentati con i diagrammi di Venn: regioni delimitate da linee circolari.

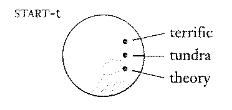
In un insieme è importante la sequenza, non l’ordine. Ne consegue che:

Sequenze e tuple

Una sequenza è una lista di oggetti in un qualche ordine

In una sequenza è importante la ripetizione (ma non lo è in un insieme). Ne consegue che: Una sequenza finita è chiamata tupla. Una sequenza con k-elementi è una k-tupla. Quindi (7, 21, 75) è una 3-tupla. Una 2-tupla è anche chiamata coppia ordinata.

Se A e B sono due insiemi, A x B è l’insieme di tutte le coppie in cui il primo elemento è un elemento di A ed il secondo è un elemento di B.

Funzioni e relazioni

Una funzione (o mappa) è un oggetto che stabilisce una relazione input-output, cioè che prende un input e restituisce un output.

L’insieme dei possibili input per la funzione è detto dominio. L’output di una funzione forma un insieme chiamato codominio o range.

Una funzione può non utilizzare tutti gli elementi del codominio specificato, una funzione che fa uso di tutti gli elementi del codominio si dice suriettiva.

Una funzione con k argomenti si dice funzione k-aria e k è chiamata arietà della funzione. Se k=1, f ha un solo argomento e sarà una funzione funzione unaria. Se k=2, f è una funzione binaria.

Un predicato o proprietà è una funzione il cui range è {VERO, FALSO}.

Grafo (Struttura dati)

Stringhe e linguaggi

Alfabeto: un qualsiasi insieme finito non vuoto. Gli elementi dell’alfabeto sono i simboli dell’alfabeto

Alcuni esempi:

La stringa su di un alfabeto è la sequenza finita di simboli dell’alfabeto, solitamente scritti uno di seguito all’altro e non separati da virgole. La stringa vuota è una stringa di lunghezza 0. La stringa z è una sottostringa di w se z appare consecutivamente a w. La concatenazione di x e y è xy, per concatenare una stringa con se stessa usiamo la notazione x^k. Stringa Una successione con un numero finito di termini è una stringa

Logica Booleana

I valori VERO e FALSO sono chiamati valori booleani e sono spesso rappresentati dai valori 1 e 0. Siamo in grado di manipolare i valori booleani mediante le operazioni booleane:

1. operazione di negazione o not; La negazione di un valore booleano è il valore opposto

2. la congiunzione o and; La congiunzione di due valori booleani è 1 se entrambi i valori sono 1

3. la disgiunzione o or; La disgiunzione di 2 valori booleani è 1 se almeno uno di questi valori è 1

4. or esclusivo o xor Dà valore 1 se esattamente uno dei due operandi è 1

5. uguaglianza E’ uno se entrambi gli operandi hanno lo stesso valore

6. implicazione E’ 0 se il suo primo operando ha valore 1 ed il suo secondo operando ha valore 0, altrimenti implica che sia 1

Esempi:

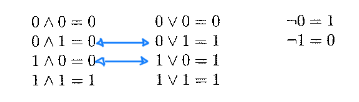
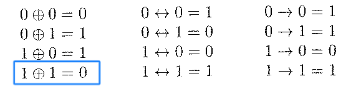
La legge distributiva risulta utile per AND e OR. E’ simile alla legge distributiva per addizione e moltiplicazione, che stabilisce che La versione booleana è disponibile in 2 forme: