Modello lineare generalizzato (GLM)

Definizione di modello lineare generalizzato

Un modello lineare generalizzato (GLM) è una generalizzazione (o estensione) del modello lineare classico nell’ambito della Regressione lineare che consente di modellare relazioni tra i predittori (le variabili indipendenti) e la variabile di risposta (la variabile dipendente).quando:

• La variabile risposta non segue la distribuzione normale;
• La relazione tra variabile risposta e le esplicative NON è necessariamente lineare (Funzione di legame)

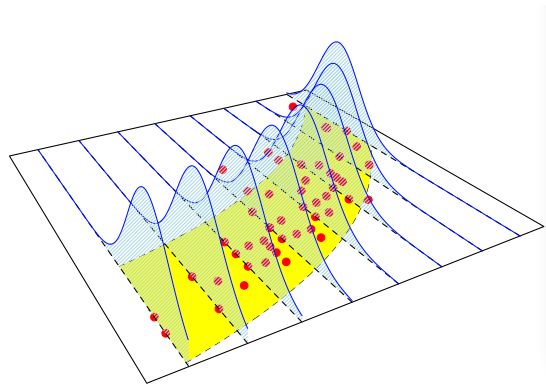Il piano orizzontale (la base): Rappresenta lo spazio definito da due variabili predittrici, chiamiamole e . Ogni punto su questo piano è una combinazione di valori di e .

• I punti rossi: Sono i dati osservati. Ogni punto ha tre coordinate , dove è il valore reale della variabile di risposta che hai misurato. Nota che i punti non giacciono su una superficie piana, ma sono sparsi.
  • Il piano giallo inclinato: Questo è il cuore del modello. Rappresenta il valore atteso (la media) della variabile di risposta, predetto dal modello per ogni combinazione dei predittori. In un GLM, questa superficie è ottenuta tramite due passaggi:
    1. Un predittore lineare: . Questa è una combinazione lineare dei predittori, che di per sé definirebbe un piano.
    2. Una funzione di legame (link function): Questa funzione collega la media della risposta al predittore lineare. Il piano giallo che vediamo è quindi la rappresentazione di , cioè la media della risposta trasformata per tornare alla sua scala originale.
  • Le curve a campana blu: Questa è la parte “Generalizzata”. A differenza di un modello lineare classico (che assume che i punti si disperdano secondo una distribuzione Normale con varianza costante attorno al piano), un GLM permette che la distribuzione della risposta appartenga ad altre famiglie (es. Poisson, Binomiale, Gamma). Le curve blu mostrano che per un dato valore dei predittori, il modello non predice un singolo punto sul piano giallo, ma una distribuzione di probabilità di cui il piano giallo rappresenta solo la media. I punti rossi (i dati reali) sono visti come un campione estratto da queste distribuzioni.

Esempi di applicazioni pratiche tramite GLM

I GLM possono gestire variabili risposta che seguono altre distribuzioni oltre quella normale:

• Conteggi: numero di clienti, numero di errori (distribuzione di Poisson).
• Proporzioni/Probabilità: successo/fallimento, sì/no (distribuzione Binomiale, come nella regressione logistica).
• Tempi di attesa: (distribuzione Gamma o Esponenziale). Di seguito alcuni esempi di GLM specifici:

• la Regressione lineare: la variabile risposta è continua e positiva, spesso asimmetrica. Assume che segua una distribuzione Gamma. Un legame comune è la funzione log: . Similmente alla regressione di Poisson, è il fattore moltiplicativo per la media . Applicazioni includono tempi, costi, e redditi.
• la Regressione logistica: la variabile risposta è binaria (es. 0 o 1). Assume che segua una distribuzione Bernoulli (o Binomiale con ). Il legame canonico è la funzione logit: . rappresenta l’odds ratio per l’aumento di un’unità in . È ampiamente usata per la classificazione binaria.
• la Regressione di Poisson: la variabile risposta è un conteggio (numeri interi non negativi). Assume che segua una distribuzione Poisson. Il legame canonico è la funzione log: . rappresenta il fattore moltiplicativo per la media quando aumenta di un’unità. È usata per modellare eventi rari o tassi di incidenza.

Funzione di legame (Statistica)

La funzione di legame (“link function” in inglese) permette di trasformare la relazioni tra le variabili: anche se i predittori sono combinati linearmente, questa combinazione lineare è poi collegata alla media della variabile risposta attraverso questa funzione di legame, permettendo di modellare relazioni che non sono una linea retta sulla scala originale della variabile risposta.

Definizione di modello lineare generalizzato (GLM)

I modelli Lineari Generalizzati (GLM) (o Generalized Linear Models in inglese) sono un framework statistico che estende il Modello lineare classico. Essi consentono di modellare relazioni tra una variabile risposta e variabili esplicative anche quando la risposta non segue una distribuzione normale o la relazione non è necessariamente lineare.

Componenti di un GLM

Un GLM è costituito da tre componenti fondamentali:

1. Componente casuale (o stocastica): specifica la distribuzione di probabilità della variabile risposta . Si assume che segua una distribuzione appartenente alla Famiglia naturale esponenziale (NEF).
   • Proprietà fondamentali: Per una variabile della famiglia esponenziale, il valore atteso e la varianza sono dati da:
     • dove e sono la prima e la seconda derivata di rispetto a . La funzione è nota come funzione di varianza, , quindi .
   • Esempi di distribuzioni: Rientrano in questa famiglia le distribuzioni Normale, Binomiale, Poisson e Gamma.
2. Componente sistematica: Le variabili esplicative producono un predittore lineare : . In notazione matriciale, si esprime come .
   • Le variabili in possono essere quantitative, categoriali o un mix. Possono essere originali o derivate tramite trasformazioni (es. logaritmi, potenze, funzioni trigonometriche) o interazioni (combinazioni di più variabili, tipicamente tramite prodotto).
   • La dimensione del modello è data dal numero di parametri nel vettore . Si distinguono modelli saturi (), ridotti () e nulli (, con come vettore di 1).

GLM vs. Trasformazione Diretta della Variabile Risposta: Una differenza cruciale tra i GLM e altri approcci (es. trasformazione di una variabile ) è che nei GLM non si trasforma direttamente la variabile risposta , ma il suo valore atteso : . Applicare una trasformazione direttamente a (es. ) può portare a incoerenze, poiché in generale . La funzione legame nei GLM mantiene la coerenza statistica, evitando errori sistematici.

Stima dei Parametri nei GLM: I parametri nei GLM sono stimati tramite il metodo della Massima verosimiglianza. Poiché le equazioni di verosimiglianza non ammettono generalmente una soluzione esplicita, è necessario ricorrere a metodi iterativi. L’algoritmo standard è l’Iterative Weighted Least Squares (IWLS), basato sul metodo di Newton-Raphson. L’IWLS risolve un problema di minimi quadrati pesati ad ogni iterazione, aggiornando iterativamente i pesi.

Diagnostica nei GLM: La diagnostica è fondamentale per valutare l’adeguatezza del modello, verificando la scelta della famiglia di distribuzione e della funzione legame, la forma funzionale del predittore lineare e la presenza di outlier o punti influenti. Si utilizzano diversi tipi di residui:

• Residui Ordinari (o di Risposta): . Hanno utilità limitata nei GLM poiché non tengono conto della funzione di link.
• Residui di Lavoro (Working Residuals): . Sono più informativi dei residui ordinari in quanto considerano la struttura del modello.
• Residui di Pearson: . Sono residui standardizzati che stimano il contributo di ogni osservazione all’adeguatezza complessiva del modello.
• Residui di Devianza: . Rappresentano il contributo individuale alla devianza complessiva del modello e tengono conto della famiglia esponenziale e del link.
• Residui Jackknife (o Predittivi): Non sono un nuovo tipo di residui, ma un modo diverso di calcolare quelli già noti, escludendo ogni osservazione a turno durante la stima per ottenere una previsione “leave-one-out”.
• Elementi di Leva (Leverages): Elementi diagonali della hat matrix , misurano quanto l’i-esima osservazione è distante dal centro dello spazio delle esplicative e il suo potenziale di influenza.
• Distanza di Cook: Misura l’influenza complessiva di un’osservazione, combinando informazioni sui residui e sui leverages.

I GLM sono strumenti versatili per l’analisi dei dati, offrendo una grande flessibilità nel modellare diversi tipi di variabili risposta e relazioni, pur mantenendo un solido fondamento statistico e interpretativo.