Alex's KB

Statistica

13 minuti

Definizione di Statistica

La statistica è una scienza che studia i fenomeni collettivi che possono presentare delle condizioni di incertezza o non determinismo (cioè di non completa conoscenza dell’evento o in sua parte).

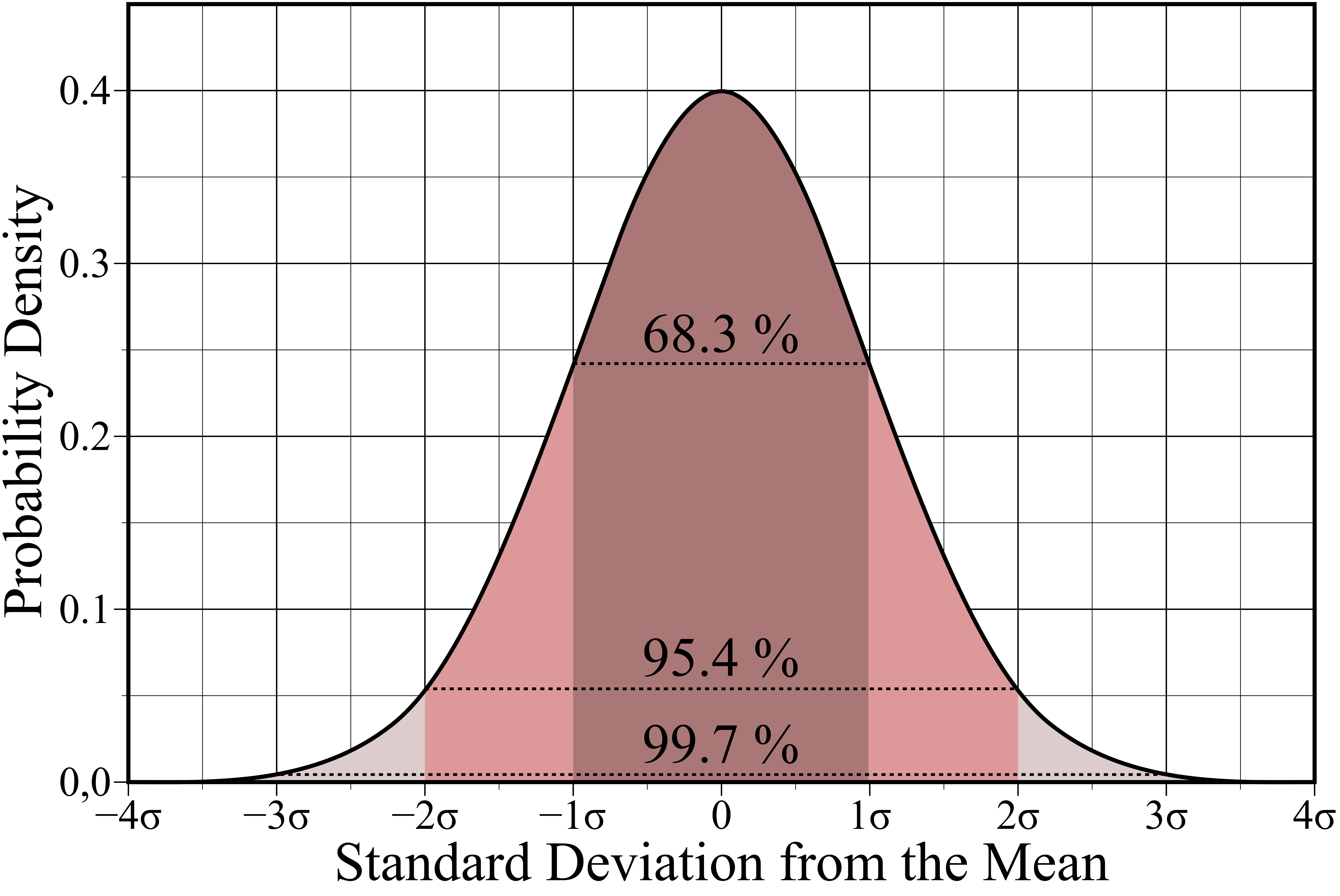
Statistica Inferenziale

Utilizza un campione per ricavare informazioni sull’intera popolazione.

  • Popolazione statistica (o Collettivo Statistico): L’intero gruppo di unità omogenee che si vuole studiare.
  • Unità Statistica: Ogni elemento della popolazione.
  • Campione: Un sottoinsieme della popolazione, scelto per riflettere la composizione della popolazione. Un campione casuale è costituito da variabili aleatorie (v.a.) indipendenti e identicamente distribuite (i.i.d.).
  • Matrice di dati: Organizzazione dei dati in righe (unità statistiche) e colonne (caratteri o variabili).
  • Tipi di Variabile statistica (o Caratteri):

Statistica Descrittiva

Si occupa della raccolta, organizzazione e descrizione dei dati. Ad esempio descrive e sintetizza le principali caratteristiche di una popolazione.

3. Associazione tra Variabili

Analizza le relazioni tra due o più variabili.

  • Distribuzioni congiunte (Tabelle a Doppia Entrata): Estensione delle distribuzioni semplici a due variabili, mostrando le frequenze per ogni coppia di modalità.
  • Indipendenza statistica e Dipendenza statistica: Due variabili sono indipendenti se la conoscenza della modalità di una non fornisce informazioni sull’altra. Le frequenze osservate in una tabella di contingenza devono rispettare .
    • Dipendenza statistica perfetta e Interdipendenza: Situazioni estreme di dipendenza.
    • Misure di Associazione (per variabili qualitative):
      • Test chi-quadro di Pearson: Misura il grado di dipendenza tra due variabili.
      • Coefficiente : Per caratteri dicotomici (binari).
      • V di Cramer: Una normalizzazione del per confrontare il grado di associazione tra tabelle di diverse dimensioni.
  • Dipendenza statistica in media: Un carattere quantitativo Y dipende in media da un carattere X se le medie condizionate di Y rispetto alle modalità di X sono diverse.
    • Varianza delle Medie Condizionate (Varianza Spiegata): Misura la variabilità tra le medie condizionate.
    • Media delle Varianze Condizionate (Varianza Residua): Misura la variabilità interna alle distribuzioni condizionate.
    • Rapporto di Correlazione (): Indice relativo di dipendenza in media, .
  • Correlazione lineare (per variabili quantitative):
    • Covarianza: Misura la variazione congiunta di due variabili.
    • Coefficiente di Correlazione Lineare di Pearson (): Indice relativo di correlazione lineare, varia tra -1 e 1.
  • Indici di Cograduazione (per variabili ordinali o quantitative trasformate in ranghi):
    • Ranghi: Posizione di un’unità in una serie ordinata.
    • di Spearman: Misura l’associazione tra due graduatorie (ranghi).
    • di Kendall: Misura la concordanza/discordanza tra le coppie di ranghi.

4. Inferenza Statistica

È il processo di generalizzazione dei risultati da un campione alla popolazione, quantificando l’incertezza.

  • Logica del Campionamento statistico: Si assume che il carattere di interesse X nella popolazione segua una distribuzione di probabilità , dove è il vettore dei parametri oggetto di inferenza.
    • Teorema del Limite Centrale (TLC): Afferma che la media campionaria () si distribuisce approssimativamente come una Normale per sufficientemente grande, indipendentemente dalla distribuzione della popolazione.
  • Stima statistica: Processo di utilizzo dei dati campionari per inferire i valori dei parametri di una popolazione.
    • Stimatore: Una funzione delle v.a. del campione usata per stimare un parametro.
    • Stima: La realizzazione numerica dello stimatore per un dato campione.
    • Proprietà degli Stimatori:
      • Non Distorsione (Correttezza): Uno stimatore è non distorto se . La differenza è chiamata Bias.
      • Efficienza: Confronta due stimatori in base al loro Errore Quadratico Medio (MSE).
      • Consistenza: Un successione di stimatori è consistente se converge in probabilità al parametro vero all’aumentare della dimensione campionaria. Richiede non distorsione asintotica e riduzione della varianza.
      • Statistiche Sufficienti: Una statistica che contiene tutte le informazioni sul parametro presenti nel campione.
    • Metodi di Costruzione degli Stimatori:
      • Metodo dei Momenti.
      • Metodo della Massima Verosimiglianza (MLE): Stima i parametri che massimizzano la probabilità di osservare i dati campionari (funzione di verosimiglianza). Il logaritmo della funzione di verosimiglianza (log-verosimiglianza) è spesso usato per facilitare i calcoli.
        • Proprietà di MLE: Invarianza, efficienza asintotica, non distorsione asintotica, consistenza, distribuzione asintoticamente Normale.
        • Informazione di Fisher: Misura la quantità di informazione che i dati campionari contengono su un parametro.
  • Intervallo di confidenza (Statistica) (IC): Forniscono un range di valori che contiene il parametro della popolazione con una certa probabilità (livello di confidenza ).
    • Ampiezza dell’IC: Dipende dalla deviazione standard del carattere (), dalla dimensione campionaria () e dal livello di confidenza ().
    • Distribuzione t di Student: Utilizzata per la costruzione di IC per la media quando la varianza della popolazione è ignota.
  • Test di ipotesi statistica: procedura per formulare un’affermazione riguardo a un parametro e analizzare i dati per valutarne il supporto.
    • Ipotesi Nulla (H0): L’affermazione da confutare (es. ).
    • Ipotesi Alternativa (H1): L’affermazione a cui si è interessati (es. ).
    • Regione di Rifiuto (o Critica): L’insieme dei valori della statistica test per cui si rifiuta H0.
    • Errori:
      • Errore di I Tipo (): Rifiutare H0 quando è vera (Falso Positivo). è il livello di significatività.
      • Errore di II Tipo (): Accettare H0 quando è falsa (Falso Negativo).
      • Potenza del Test (): La probabilità di rifiutare correttamente H0 quando è falsa.
    • Statistica Test: Una metrica per l’effetto di interesse (es. Z-statistic, t-statistic).
    • Approcci al Test: Approccio del Valore Critico e Approccio del p-value.
      • p-value: La probabilità di osservare un risultato uguale o più estremo di quello ottenuto, assumendo che H0 sia vera.
    • Multiple Testing: Il problema che sorge quando si testano molte ipotesi contemporaneamente, aumentando la probabilità di falsi positivi.
      • Family-Wise Error Rate (FWER): La probabilità di commettere almeno un errore di I tipo in una famiglia di test.
      • False Discovery Rate (FDR): La proporzione attesa di falsi positivi tra le ipotesi rifiutate.
      • Metodi di Controllo: Bonferroni, Holm, Benjamini-Hochberg.

5. Modelli di Regressione e Classificazione

Un insieme di strumenti per la previsione e l’inferenza, basati sulle relazioni tra variabili.

  • Regressione Lineare: Modella la relazione lineare tra una variabile di risposta quantitativa e una o più variabili predittive.
    • Regressione Lineare Semplice: Un solo predittore.
    • Regressione Lineare Multipla: Più predittori.
    • Metodo dei Minimi Quadrati Ordinari (OLS): Stima i coefficienti minimizzando la somma dei quadrati dei Residui statistici (differenza tra valori osservati e stimati).
    • Residui statistici: Gli scarti tra i valori osservati e i valori stimati, importanti per la diagnostica del modello.
    • Scomposizione della Devianza: La devianza totale della risposta Y può essere scomposta in devianza spiegata (dalla regressione) e devianza residua.
    • Assunzioni del modello: Linearità, indipendenza degli errori, omoschedasticità (varianza costante degli errori). L’assunzione di normalità degli errori permette l’inferenza sui parametri.
    • Predittori Qualitativi: Gestiti tramite variabili dummy (indicatori binari).
    • Interazioni: Effetti combinati di due o più predittori.
  • Modello lineare generalizzato (GLM) (GLM): Estendono il modello lineare classico per trattare risposte non normali, unificando regressione lineare, logistica, di Poisson, ecc..
  • Classificazione statistica: Assegna osservazioni a classi predefinite.
    • Matrice di Confusione: Tabella che riassume le performance di un classificatore (veri/falsi positivi/negativi).
    • Metriche di Performance: Precisione, Recall (Sensibilità), Specificità, F1-Score.
    • Soglia di Decisione: Determina la classificazione basata sul punteggio di probabilità.
    • Curve ROC (Receiver Operating Characteristic) e PR (Precision-Recall): Visualizzano le performance del classificatore a diverse soglie.
    • Training set e Test Set: Divisione dei dati per addestrare e valutare il modello, prevenendo l’overfitting.
    • Cross-Validation (K-fold CV): Tecnica robusta per valutare la generalizzabilità del modello, dividendo i dati in sottoinsiemi (fold).
    • Overfitting: Quando un modello si adatta troppo bene ai dati di training, perdendo capacità di generalizzazione.
    • Bias-Variance Trade-off: Concetto fondamentale nell’apprendimento statistico, che spiega come modelli più flessibili tendano ad avere bias basso e varianza alta, e viceversa.
  • Regressione Logistica: Modello GLM per variabili di risposta binarie (es. 0/1).
    • Odds e Odds ratio (OR): Rapporto tra probabilità, e rapporto tra odds, per quantificare l’associazione tra variabili.
    • Logit: Funzione di legame canonica per la distribuzione binomiale.
    • Interpretazione dei Coefficienti: I coefficienti sono log-odds ratio, sono odds ratio.
  • Regressione multinomiale: Estensione della regressione logistica per variabili di risposta categoriche con più di due categorie non ordinali.
    • Categoria di Riferimento: Una categoria base rispetto alla quale vengono calcolati i log-odds ratio delle altre categorie.
  • Analisi del discriminante (DA): Tecnica statistica per la classificazione che cerca funzioni discriminanti per separare le classi, basata sul Teorema di Bayes.
    • Assunzione di Normalità Condizionale: Le variabili esplicative X, condizionate alla classe Y, seguono una distribuzione Normale Multivariata.
    • Linear Discriminant Analysis (LDA): Assume che tutte le classi abbiano la stessa matrice di covarianza (Σ), risultando in confini di decisione lineari. Utilizzabile anche per riduzione della dimensionalità (Criterio di Fisher).
    • Quadratic Discriminant Analysis (QDA): Permette a ogni classe di avere la propria matrice di covarianza (Σk), risultando in confini di decisione quadratici.
  • Naive Bayes: Classificatore probabilistico basato sul Teorema di Bayes, che assume l’indipendenza condizionale tra le caratteristiche data la classe (“ingenua”).
    • Smoothing (Laplace Smoothing): Tecnica per evitare probabilità nulle se una categoria non appare nei dati di training.
    • Varianti: Gaussian Naive Bayes (per caratteristiche continue), Multinomial Naive Bayes (per conteggi, es. bag-of-words), Bernoulli Naive Bayes (per caratteristiche binarie).
  • K-Nearest Neighbors (KNN): Un metodo non parametrico molto semplice per la classificazione (e regressione), che classifica un punto basandosi sui k punti più vicini nel training set.

6. Tecniche di Selezione e Riduzione della Dimensionalità

Gestiscono il numero di predittori e la loro struttura.

  • Selezione di Sottogruppi (Subset Selection):
    • Best Subset Selection: Esamina tutti i possibili modelli con un dato numero di predittori.
    • Stepwise Selection: Approcci iterativi (Forward, Backward) per aggiungere/rimuovere predittori.
  • Metodi di Shrinkage (Regolarizzazione): Riducono i coefficienti di regressione verso zero per migliorare la predizione e l’interpretabilità, specialmente in alta dimensionalità.
    • Ridge Regression: Applica una penalità L2 alla somma dei quadrati dei coefficienti, riducendoli ma non azzerandoli.
    • The Lasso: Applica una penalità L1 alla somma dei valori assoluti dei coefficienti, potendo azzerare alcuni di essi e favorendo la selezione di variabili.
  • Metodi di Riduzione della Dimensionalità: Trasformano i predittori originali in un insieme più piccolo di nuove variabili.
    • Principal Components Regression (PCR): Utilizza i primi M componenti principali come predittori in un modello di regressione lineare.
    • Partial Least Squares (PLS): Un’alternativa alla PCR.
    • Considerazioni in Alte Dimensioni: Problemi e sfide quando il numero di caratteristiche () è molto maggiore del numero di osservazioni ().
  • Principal Components Analysis (PCA): Tecnica di apprendimento non supervisionato per riassumere un ampio insieme di variabili correlate con un numero minore di variabili rappresentative (componenti principali).
    • Concetto: Il primo componente principale indica la direzione in cui i dati variano di più.
    • Loading Vectors e Score Vectors: I loadings definiscono la direzione dei componenti, gli scores sono i valori delle osservazioni proiettate su tali direzioni.
    • Proporzione di Varianza Spiegata (PVE): Misura quanta variabilità dei dati originali è catturata da ciascun componente principale.
    • Scree Plot: Grafico che mostra la PVE per ciascun componente, utile per decidere quanti componenti mantenere.
    • Usi: Riduzione della dimensionalità, visualizzazione dei dati, imputazione dei dati mancanti.
  • Analisi delle Corrispondenze (Correspondence Analysis): Tecnica simile alla PCA, ma per matrici di incidenza o tabelle di contingenza (dati categorici).

7. Apprendimento Non Supervisionato

Si concentra sulla scoperta di relazioni e strutture nei dati senza un output predefinito.

  • Clustering: Raggruppa le osservazioni in sottogruppi (cluster) omogenei.
    • K-Means Clustering: Partiziona i dati in K cluster, dove ogni osservazione appartiene al cluster con la media più vicina. La scelta di K è una questione pratica.
    • Hierarchical Clustering: Costruisce una gerarchia di cluster. Può essere agglomerativo (bottom-up, partendo da singoli punti e fondendo i più simili) o divisivo.
      • Metodi di Linkage: Definiscono la dissimilarità tra cluster (Complete, Average, Single, Centroid).
      • Dendrogramma: Rappresentazione grafica della struttura gerarchica dei cluster.
  • Missing Values and Matrix Completion: Gestione dei dati mancanti, che sono comuni nei dataset reali.

8. Argomenti Speciali

  • Modelli Oltre la Linearità (Non-linear Models): Estendono la regressione lineare per catturare relazioni più complesse.
    • Basis Functions: Trasformazioni non lineari delle variabili predittive che permettono di adattare modelli lineari a relazioni non lineari (es. regressione polinomiale).
    • Splines: Funzioni piecewise polinomiali che offrono maggiore flessibilità rispetto ai polinomi globali (es. Cubic Splines, Natural Splines, Smoothing Splines).
    • Local Regression (LOESS): Stima la funzione f localmente, adattando un modello semplice (es. lineare) a sottosezioni dei dati.
    • Generalized Additive Models (GAMs): Estendono i GLM consentendo che il predittore lineare sia una somma di funzioni non lineari delle covariate.
  • Analisi della Sopravvivenza e Dati Censurati: Gestisce dati in cui la variabile output (es. tempo di un evento) può essere censurata, cioè non completamente osservata.
    • Hazard Function e Survivor Function: Funzione matematica chiave per descrivere il rischio di un evento e la probabilità di sopravvivenza nel tempo.
    • Cox’s Proportional Hazards Model: Un modello ampiamente utilizzato per l’analisi di sopravvivenza.
    • Kaplan-Meier Estimator: Stima non parametrica della funzione di sopravvivenza.
  • Deep Learning e Reti Neurali: (Menziato come parte dell’IDA, ma non approfondito nelle fonti). Concetti come bag-of-words per l’elaborazione del linguaggio.
  • Analisi delle Serie Storiche (Time Series Analysis): (Menziato come parte dell’IDA, ma non approfondito nelle fonti) Analisi di dati sequenziali, spesso con dinamiche lineari o non lineari.
  • Fuzzy Logic: (Menziato come parte dell’IDA, ma non approfondito nelle fonti) Approccio per gestire l’incertezza e la vaghezza nei dati, contrapposto alla probabilità “crisp”.

Strumenti Software e Data Set:

  • Le fonti fanno riferimento all’uso di R e Python con pacchetti come ISLR2, MASS, seaborn.

  • Sono menzionate numerose funzioni R per l’analisi e la visualizzazione (summary(), pairs(), plot(), range(), mean(), sd(), dim(), na.omit(), lm(), coef(), prcomp(), hclust(), glm(), t.test(), lda(), qda(), naiveBayes(), randomForest(), svm(), kmeans()).

  • Vengono utilizzati vari Data Set per esempi pratici ed esercitazioni: Advertising, Auto, Bikeshare, Boston, BrainCancer, Caravan, Carseats, College, Credit, Default, Fund, Hitters, Khan, NCI60, NYSE, OJ, Penguins, Portfolio, Publication, Smarket, Tips, USArrests, Wage, Weekly, Wine_data, Diamonds.

    Questo quadro dovrebbe fornirti una base solida per il tuo studio, evidenziando le interconnessioni tra i vari concetti e la loro rilevanza pratica nell’analisi dei dati.

Vista grafico

Link entranti